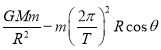Question

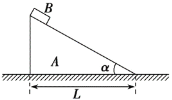
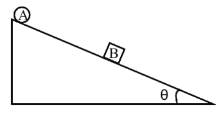
【题目】水平面上固定着倾角θ＝30°斜边长为 L=5m 的斜面，小球A质量mA，小物块B质量mB，A球自斜面顶端无初速度释放，B静止在斜面中点。已知B与斜面间摩擦因数，重力加速度大小 g＝10m/s2，忽略A球的滚动摩擦，A、B碰撞时间极短且为弹性碰撞。求

(1)A 与 B 碰前的速度 v0；

(2)为使 A、B 能在斜面上发生两次及以上碰撞，则的取值范围。

Answer 1

【答案】(1)5m/s；(2)

【解析】

(1)根据牛顿第二定律

根据速度位移方程

(2)A、B发生弹性碰撞，根据动量守恒

根据机械能守恒

解得

因为B与斜面间摩擦因数，所以碰后B做匀速运动，碰后到达斜面底端时间

在此时间内A需重新追上B，设恰好在斜面最低点追上，则

所以当（也正确）时可在斜面上发生二次以上碰撞。