题目内容
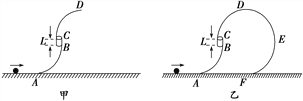
【题目】如图甲所示,弯曲部分AB和CD是两个半径都为0.3 m的![]() 圆弧轨道,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)轨道,分别与上下圆弧轨道相切连接,BC段的长度L为0.2 m.下圆弧轨道与水平轨道相切,其中D、A分别是上下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内.有一质量为0.3 kg的小球以一定的速度沿水平轨道向右运动并从A点进入圆弧,不计小球运动中的一切阻力,求:
圆弧轨道,中间的BC段是竖直的薄壁细圆管(细圆管内径略大于小球的直径)轨道,分别与上下圆弧轨道相切连接,BC段的长度L为0.2 m.下圆弧轨道与水平轨道相切,其中D、A分别是上下圆弧轨道的最高点与最低点,整个轨道固定在竖直平面内.有一质量为0.3 kg的小球以一定的速度沿水平轨道向右运动并从A点进入圆弧,不计小球运动中的一切阻力,求:
(1)如果小球从D点以5 m/s的速度水平飞出,求落地点与D点的水平距离;
(2)如果小球从D点以5 m/s的速度水平飞出,求小球过圆弧A点时对轨道的压力;
(3)如果在D点右侧平滑连接一半径R=0.4 m的半圆形光滑轨道DEF,如图乙所示,要使小球不脱离轨道运动,求小球在水平轨道上向右运动的速度大小范围(计算结果可以用根式表示).
【答案】(1)2 m (2)44 N (3) ![]() 或
或![]()
【解析】试题分析:(1)小球从D点以5m/s的速度水平飞出后做平抛运动,由平抛运动规律可得:h=![]() gt2
gt2
据题 h=2R+L=2×0.3m+0.2m=0.8m
代入数据解得 t=0.4s
所以落地点与D点的水平距离 x=vDt=5×0.4m=2m;
(2)由A到D的过程,由机械能守恒定律可得:mgh+![]() mvD2=
mvD2=![]() mvA2
mvA2
在A点,由牛顿第二定律可得: ![]() ;
;
联立解得 N=94N
由牛顿第三定律知,小球过圆弧A点时对轨道的压力 N′=N=94N
(3)计论一:
小球进入轨道最高运动到C点,之后原路返回,由机械能守恒定律,有:
mg(R+L)=![]() mv12
mv12
得 v1=![]() m/s
m/s
讨论二:小球进入轨道后恰好能通过圆弧最高点D,之后沿DEF运动而不脱离轨道,在D点,有
![]()
从A到D由机械能守恒定律可得:
有:mgh+![]() mv2=
mv2=![]() mv22
mv22
得![]()
所以要使小球在运动过程中能不脱离轨道,初速度大小的范围为:v1≤![]() m/s或v2≥
m/s或v2≥![]() m/s
m/s

 阅读快车系列答案
阅读快车系列答案