题目内容
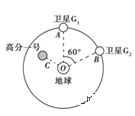
【题目】如图为高分一号北斗导航系统两颗卫星在空中某一面内运动的示意图。导航卫星G1和G2以及高分一号均可认为统地心0做匀速圆同运动。卫星G1和G2的轨道半径为r，某时刻两颗导航卫星分别位于轨道上的A和B两位置，高分一号在C位置。若卫星均顺时针运行，∠AOB=60°，地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力。则下列说法正确的是
A. 卫星G1和G2的加速度大小相等且为 
B. 卫星G1由位置A运动到位置B所需的时间为
C. 若高分一号与卫星G1的周期之比为1:k(k＞1,且为整数),某时刻两者相距最近，则从此时刻起,在卫星G1运动一周的过程中二者距离最近的次数为（k-1）
D. 若高分一号与卫星G1质量相等,由于高分一号的绕行速度大,则发射所需的最小能量更多
【答案】BC
【解析】
卫星在地球表面时受到的万有引力等于重力，则：mg=
；在太空运行时：
＝ma，所以：a=
g．故A错误；根据万有引力提供向心力=mω2r，得
，卫星G1由位置A运动到位置B所需的时间
，故B正确；设每隔时间T，a、b相距最近，则（ωa-ωb）T=2π，所以有：
；故b运动一周的过程中，a、b相距最近的次数为：n=
=k-1，即a、b距离最近的次数为k-1次，故C正确； 发射的卫星轨道越高，需要的能量越大，由于高分一号的轨道低一些，所以它与卫星G1相比，发射所需的最小能量更小。故D错误；故选BC。
练习册系列答案
相关题目
