题目内容
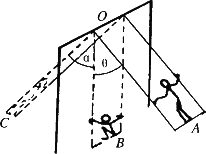
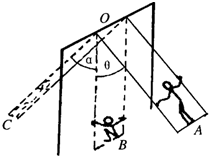
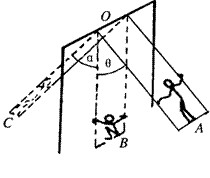
如图是荡秋千的示意图．最初人直立站在踏板上，两绳与竖直方向的夹角均为θ，人的重心到悬点O的距离为l1；从A点向最低点B运动的过程中，人由直立状态自然下蹲，在B点人的重心到悬点O的距离为l2；在最低点处，人突然由下蹲状态变成直立状态（人的重心到悬点O的距离恢复为l1），且保持该状态到最高点C．设人的质量为m，不计踏板和绳的质量、不计一切摩擦和空气阻力，求（1）人第一次到达最低点B还处于下蹲状态时，两根绳的总拉力F为多大？
（2）人第一次到达最高点C时，绳与竖直方向的夹角α为多大？（可用反三角函数表示；解答本问时可不考虑超重和失重）
【答案】分析：（1）人由A点向B点（还处于下蹲状态时）的过程中，只有重力做功，运用机械能守恒求出到达B点时的速度大小，由牛顿第二定律列式求拉力F．
（2）人从B点保持直立状态到达C点的过程中，根据机械能守恒求解α．
解答：解：（1）人由A点向B点（还处于下蹲状态时）的过程中，
根据机械能守恒得，mg（l2-l1cosθ）=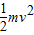
在最低点B，F-mg=m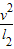
解得F=（3-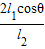
）mg
（2）人从B点保持直立状态到达C点的过程中，根据机械能守恒得，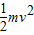
=mgl1（1-cosα）
解得α=arccos（cosθ-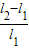
）
答：
（1）人第一次到达最低点B还处于下蹲状态时，两根绳的总拉力F为（3-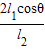
）mg．
（2）人第一次到达最高点C时，绳与竖直方向的夹角α为arccos（cosθ-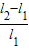
）．
点评：本题是实际问题，要建立模型，将实际问题进行简化，再运用机械能守恒和牛顿定律结合进行处理．
（2）人从B点保持直立状态到达C点的过程中，根据机械能守恒求解α．
解答：解：（1）人由A点向B点（还处于下蹲状态时）的过程中，
根据机械能守恒得，mg（l2-l1cosθ）=
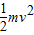
在最低点B，F-mg=m
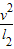
解得F=（3-
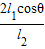）mg（2）人从B点保持直立状态到达C点的过程中，根据机械能守恒得，
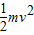=mgl1（1-cosα）解得α=arccos（cosθ-
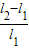）答：
（1）人第一次到达最低点B还处于下蹲状态时，两根绳的总拉力F为（3-
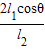）mg．（2）人第一次到达最高点C时，绳与竖直方向的夹角α为arccos（cosθ-
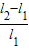）．点评：本题是实际问题，要建立模型，将实际问题进行简化，再运用机械能守恒和牛顿定律结合进行处理．
练习册系列答案
经典密卷系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
如图是荡秋千的示意图．最初人直立站在踏板上，两绳与竖直方向的夹角均为θ，人的重心到悬点O的距离为l1；从A点向最低点B运动的过程中，人由直立状态自然下蹲，在B点人的重心到悬点O的距离为l2；在最低点处，人突然由下蹲状态变成直立状态（人的重心到悬点O的距离恢复为l1），且保持该状态到最高点C．设人的质量为m，不计踏板和绳的质量、不计一切摩擦和空气阻力，求
