题目内容
如图15所示,AB和CD是足够长的平行光滑导轨,其间距为l,导轨平面与水平面的夹角为θ.整个装置处在磁感应强度为B,方向垂直于导轨平面向上的匀强磁场中.AC端连有电阻值为R的电阻.若将一质量M,垂直于导轨的金属棒EF在距BD端s处由静止释放,在EF棒滑至底端前会有加速和匀速两个运动阶段.今用大小为F,方向沿斜面向上的恒力把EF棒从BD位置由静止推至距BD端s处,突然撤去恒力F,EF最后又回到BD端.求:

(1)EF棒下滑过程中的最大速度.
(2)EF棒自BD端出发又回到BD端的整个过程中,有多少电能转化成了内能(金属棒、导轨的电阻均不计

(1)EF棒下滑过程中的最大速度.
(2)EF棒自BD端出发又回到BD端的整个过程中,有多少电能转化成了内能(金属棒、导轨的电阻均不计
(1)如图当EF从距BD端s处由静止开始滑至BD的过程中,受力情况如图所示.安培力:F安=BIl=B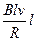
根据牛顿第二定律:a=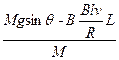 ①
①
所以,EF由静止开始做加速度减小的变加速运动.当a=0时速度达到最大值vm.
由①式中a=0有:Mgsinθ-B2l2vm/R="0 " ②
vm=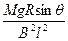
(2)由恒力F推至距BD端s处,棒先减速至零,然后从静止下滑,在滑回BD之前已达最大速度vm开始匀速.
设EF棒由BD从静止出发到再返回BD过程中,转化成的内能为ΔE.根据能的转化与守恒定律:
Fs-ΔE=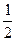 Mvm2 ③
Mvm2 ③
ΔE=Fs-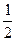 M(
M(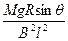 )2
)2
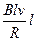
根据牛顿第二定律:a=
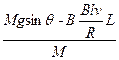 ①
①所以,EF由静止开始做加速度减小的变加速运动.当a=0时速度达到最大值vm.
由①式中a=0有:Mgsinθ-B2l2vm/R="0 " ②
vm=
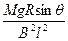
(2)由恒力F推至距BD端s处,棒先减速至零,然后从静止下滑,在滑回BD之前已达最大速度vm开始匀速.
设EF棒由BD从静止出发到再返回BD过程中,转化成的内能为ΔE.根据能的转化与守恒定律:
Fs-ΔE=
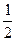 Mvm2 ③
Mvm2 ③ΔE=Fs-
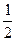 M(
M(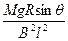 )2
)2略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,带电量|q|
,带电量|q| .求
.求




 恒定的角速度ω绕垂直于磁场方向的固定轴转动,线圈匝数n=200。穿过每匝线圈的磁通量Φ随时间按正弦规律变化,如图所示。发电机内阻,r=5.0Ω,外电路电阻R=95Ω。求:
恒定的角速度ω绕垂直于磁场方向的固定轴转动,线圈匝数n=200。穿过每匝线圈的磁通量Φ随时间按正弦规律变化,如图所示。发电机内阻,r=5.0Ω,外电路电阻R=95Ω。求: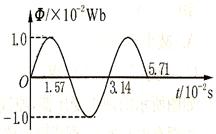
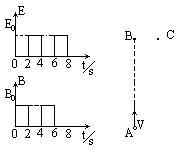
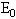 和
和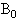 的比值.
的比值.