题目内容
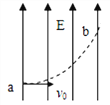
【题目】如图所示,MN 是一条通过透明球体球心 O 的直线,在真空中波长为 λ0=564nm 的单色 细光束 AB 平行于 MN 射向球体,B 为入射点,若出射光线 CD 与 MN 的交点 P 到球心 O 的距离是球半径的![]() 倍,且与 MN 所成的夹角 α=30°.求:
倍,且与 MN 所成的夹角 α=30°.求:

①透明球体的折射率n;
②此单色光在透明球体中的波长λ.
【答案】(1) ![]() (2)λ=399nm
(2)λ=399nm
【解析】①连接OB、BC,在B点光线的入射角、折射角分别标为i、r,如图所示:
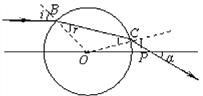
在△OCP中,由题意有:OP=OC,α=30°
解得:∠OCP=135°(45°值舍去)
可得:∠COP=180°-α-∠OCP=180°-135°-30°=15°
光线从B点射入,由折射定律有: ![]()
光线从C点射出,由折射定律有: ![]()
又∠BCO=r所以,i=45°
又∠BOC=180°-i-∠COP=120°=180°-45°-15°=120°,
故得: ![]()
因此,透明体的折射率![]()
②因为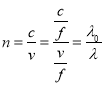 ,所以
,所以![]()

 阅读快车系列答案
阅读快车系列答案【题目】某实验小组想描绘标有“4V2W”的小灯泡的![]() 图像,除导线和开关外还备有以下器材可供选择:
图像,除导线和开关外还备有以下器材可供选择:
A.电流表![]() (量程0.6
(量程0.6![]() ,内阻约为1
,内阻约为1![]() )
)
B.电流表![]() (量程3.0A,内阻约为0.2
(量程3.0A,内阻约为0.2![]() )
)
C.电压表![]() (量程5.0V,内阻约为5k
(量程5.0V,内阻约为5k![]() )
)
D.电压表![]() (量程15.0V,内阻约为15
(量程15.0V,内阻约为15![]() )
)
E.滑动变阻器![]() (最大阻值为5
(最大阻值为5![]()
![]() ,额定电流500
,额定电流500![]() )
)
F.滑动变阻器![]() (最大阻值为10
(最大阻值为10![]() ,额定电流2.0A)
,额定电流2.0A)
G.电源(电动势为6.0V,内阻约为0.5![]() )
)
(1)实验中所用的电流表应选________;电压表应选________;滑动变阻器应选________.
(2)在虚线框内画出实验的电路图___________。
(3)经过正确的操作,测得的数据如下表,请根据下表数据在下方坐标系中描点画出小灯泡的![]() 曲线_________。
曲线_________。
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 0 | 0.40 | 0.80 | 1.20 | 1.60 | 2.00 | 2.40 | 2.80 | 3.20 | 3.60 | 4.00 |
| 0 | 0.12 | 0.22 | 0.30 | 0.36 | 0.40 | 0.43 | 0.46 | 0.48 | 0.49 | 0.50 |