题目内容
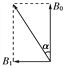
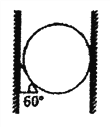
【题目】在两固定的竖直挡板间有一表面光滑的重球，球的直径略小于挡板间的距离，用一横截面为直角三角形的楔子抵住。楔子的底角为60°，重力不计。设最大静摩擦力等于滑动摩擦力。为使球不下滑，楔子与挡板间的动摩擦因数至少应为
A. 
B. 
C. 
D. 
【答案】A
【解析】设球的质量为M，隔离光滑均匀圆球，对球受力分析如图所示，由几何关系可知，θ=30°，可得：FN=Fcosθ；Mg-Fsinθ=0；解得： 
；
再以楔子为研究对象，由于其质量忽略不计，所以只受到球的压力、墙壁的支持力和摩擦力，如图：
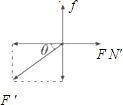
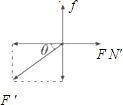
由共点力平衡可得：FN′=F′cosθ；f-F′sinθ=0
其中F′与F大小相等，方向相反．又：f=μFN′
联立得： 
．故A正确，BCD错误．故选A
练习册系列答案
相关题目
