题目内容
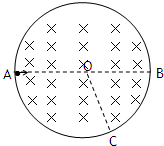 如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过△t时间从C点射出磁场,OC与OB成60°角.现将带电粒子的速度变为
如图所示,圆形区域内有垂直于纸面向里的匀强磁场,一个带电粒子以速度v从A点沿直径AOB方向射入磁场,经过△t时间从C点射出磁场,OC与OB成60°角.现将带电粒子的速度变为| v | 3 |
2△t
2△t
.分析:粒子在匀强磁场做匀速圆周运动,运动周期T=
,与粒子速度大小无关,可见,要计算粒子在磁场中运动的时间,只要求得它在磁场中运动轨迹对应的圆心角,就可得到所用的时间.
| 2πm |
| qB |
解答: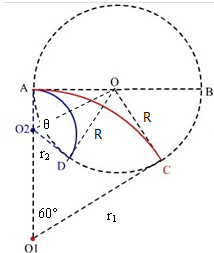 解:设圆形磁场区域的半径是R,
解:设圆形磁场区域的半径是R,
以速度v射入时,半径r1=
,
根据几何关系可知,
=tan60°,所以r1=
R;
运动时间△t=
T=
T;
以速度
射入时,半径r2=
=
r1=
R
设第二次射入时的圆心角为θ,根据几何关系可知:
tan
=
=
所以 θ=120°
则第二次运动的时间为:t=′
T=
T=
T=2△t
故答案为:2△t.
 解:设圆形磁场区域的半径是R,
解:设圆形磁场区域的半径是R,以速度v射入时,半径r1=
| mv |
| qB |
根据几何关系可知,
| r1 |
| R |
| 3 |
运动时间△t=
| 60° |
| 360° |
| 1 |
| 6 |
以速度
| v |
| 3 |
m?
| ||
| qB |
| 1 |
| 3 |
| ||
| 3 |
设第二次射入时的圆心角为θ,根据几何关系可知:
tan
| θ |
| 2 |
| R |
| r2 |
| 3 |
所以 θ=120°
则第二次运动的时间为:t=′
| θ |
| 2π |
| 120° |
| 360° |
| 1 |
| 3 |
故答案为:2△t.
点评:带电粒子在磁场中运动的题目解题基本步骤为:定圆心、画轨迹、求半径,同时还利用圆弧的几何关系来帮助解题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
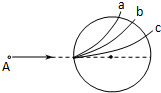 如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,下列说法正确的是( )
如图所示,圆形区域内有垂直纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同的速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图所示.若带电粒子只受磁场力作用,下列说法正确的是( )| A、a粒子动能最小 | B、b粒子运动轨道半径最大 | C、c粒子在磁场中运动时间最长 | D、它们做圆周运动的周期Ta=Tb=Tc |
 (2010?长春一模)如图所示,圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子(不计重力)以某一初速度沿圆的直径方向射入磁场,粒子穿过此区域的时间为t,粒子飞出此区域时速度方向偏转60°角,根据上述条件可求下列物理量中的( )
(2010?长春一模)如图所示,圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,一带电粒子(不计重力)以某一初速度沿圆的直径方向射入磁场,粒子穿过此区域的时间为t,粒子飞出此区域时速度方向偏转60°角,根据上述条件可求下列物理量中的( )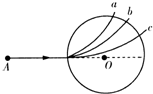 (2011?淮南一模)如图所示,圆形区域内有垂直于纸面第匀强磁场,三个质量和电量都相同第带电粒子a、b、c,以不同速率对准圆心O沿AO方向射入电场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )
(2011?淮南一模)如图所示,圆形区域内有垂直于纸面第匀强磁场,三个质量和电量都相同第带电粒子a、b、c,以不同速率对准圆心O沿AO方向射入电场,其运动轨迹如图所示.若带电粒子只受磁场力作用,则下列说法正确的是( )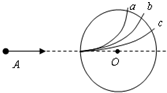 如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( )
如图所示,圆形区域内有垂直于纸面的匀强磁场,三个质量和电荷量都相同的带电粒子a、b、c,以不同速率对准圆心O沿着AO方向射入磁场,其运动轨迹如图.若带电粒子只受磁场力作用,则下列说法正确的是( ) 如图所示,圆形区域内有垂直纸而向里的匀强磁场,磁感应强度为B,一带电粒子(不计重力)以某一初速度沿圆的直径方向射入磁场,粒子穿过此区域的时间为t,粒子飞出此区域时速度方向偏转角为60°,根据上条件可求下列物理量中的
如图所示,圆形区域内有垂直纸而向里的匀强磁场,磁感应强度为B,一带电粒子(不计重力)以某一初速度沿圆的直径方向射入磁场,粒子穿过此区域的时间为t,粒子飞出此区域时速度方向偏转角为60°,根据上条件可求下列物理量中的