题目内容
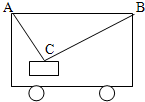如图所示，物块的质量为m，车静止时绳AC、BC与水平方向的夹角分别为53°和37°，求：（1）当车以a=0.5g的加速度向右运动时，求AC绳的拉力TA？
（2）当车以a=2g的加速度向右运动时，求BC绳的拉力TB？
分析：当AC绳拉力刚好为0时，物块在BC绳的拉力与重力的作用下，做水平加速运动，求出此时的临界加速度
判断小车加速度与临界加速度的大小关系，判断两绳受力与否，根据平衡方程和牛顿第二定律，从而求出绳的拉力
判断小车加速度与临界加速度的大小关系，判断两绳受力与否，根据平衡方程和牛顿第二定律，从而求出绳的拉力
解答：
解：当AC绳拉力刚好为0时，设车的加速度为a0．
mgtg530=ma0
求解得：a0=
g
（1）a=0.5g＜a0 时，两绳均有弹力．
TBcos37°-TAcos53°=ma
TBsin37°+TAsin53°=mg
联立求解得：TA=0.5mg TB=mg
（2）a=2g＞a0 时，物体向上飞起来，AC松弛，
BC绳有弹力TB′．
=ma
则：TB′=
mg．
答：（1）当车以a=0.5g的加速度向右运动时，AC绳的拉力为0.5mg
（2）当车以a=2g的加速度向右运动时，求BC绳的拉力为
mg
解：当AC绳拉力刚好为0时，设车的加速度为a0．mgtg530=ma0
求解得：a0=
| 4 |
| 3 |
（1）a=0.5g＜a0 时，两绳均有弹力．
TBcos37°-TAcos53°=ma
TBsin37°+TAsin53°=mg
联立求解得：TA=0.5mg TB=mg
（2）a=2g＞a0 时，物体向上飞起来，AC松弛，
BC绳有弹力TB′．
| TB/2-m2g2 |
则：TB′=
| 5 |
答：（1）当车以a=0.5g的加速度向右运动时，AC绳的拉力为0.5mg
（2）当车以a=2g的加速度向右运动时，求BC绳的拉力为
| 5 |
点评：本题关键是先找到当AC绳拉力刚好为0时，小车做水平加速运动的临界加速度，根据加速度与临界加速度的大小关系，判断绳子受力情况，根据牛顿第二定律列式求解．
练习册系列答案
相关题目
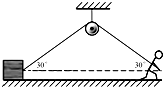如图所示，物块的质量m=30kg，细绳一端与物块相连，另一端绕过光滑的轻质定滑轮，当人用100N的力斜向下拉绳子时，滑轮两侧细绳与水平方向的夹角均为30°，物体在水平面上保持静止，滑轮上端的悬绳竖直（取g=10m/s2）．
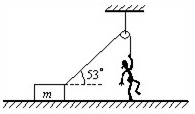如图所示，物块的质量m=30kg，细绳一端与物块相连，另一端绕过光滑的轻质定滑轮，当人用100N的力竖直向下拉绳子时，滑轮左侧细绳与水平方向的夹角为53°，物体在水平面上保持静止． 已知sin53°=0.8，cos53°=0.6，取g=10m/s2，求：
