题目内容
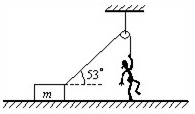 如图所示,物块的质量m=30kg,细绳一端与物块相连,另一端绕过光滑的轻质定滑轮,当人用100N的力竖直向下拉绳子时,滑轮左侧细绳与水平方向的夹角为53°,物体在水平面上保持静止. 已知sin53°=0.8,cos53°=0.6,取g=10m/s2,求:
如图所示,物块的质量m=30kg,细绳一端与物块相连,另一端绕过光滑的轻质定滑轮,当人用100N的力竖直向下拉绳子时,滑轮左侧细绳与水平方向的夹角为53°,物体在水平面上保持静止. 已知sin53°=0.8,cos53°=0.6,取g=10m/s2,求:(1)地面对物体的弹力大小和摩擦力大小;
(2)滑轮对中轴的作用力大小.
分析:(1)要求地面对物体的弹力大小和摩擦力大小可以以物块为研究对象并进行受力分析,根据物块处于平衡状态即物块所受合力为0列方程即可求解.在竖直方向有N+Tsin53°-mg=0,在水平方向有f=Tcos53,联立即可求得.
(2)由于滑轮是轻质的滑轮,所以绳子对滑轮的力多大,滑轮对中轴的力就有多大,所以要求滑轮对中轴的作用力,可以先求绳子对滑轮的力,而绳子对滑轮的力等于两边绳子拉力的合力,而求两边绳子拉力的合力可以先将左边绳子的拉力分解为水平向左的分力Tcos53?,竖直向下的分力Tsin53?,
故两根绳子对滑轮向下的拉力为(T+Tsin53?),所以可以根据勾股定理求出两根绳子对滑轮的合力
F=
,从而求出滑轮对中轴的作用力的大小.
(2)由于滑轮是轻质的滑轮,所以绳子对滑轮的力多大,滑轮对中轴的力就有多大,所以要求滑轮对中轴的作用力,可以先求绳子对滑轮的力,而绳子对滑轮的力等于两边绳子拉力的合力,而求两边绳子拉力的合力可以先将左边绳子的拉力分解为水平向左的分力Tcos53?,竖直向下的分力Tsin53?,
故两根绳子对滑轮向下的拉力为(T+Tsin53?),所以可以根据勾股定理求出两根绳子对滑轮的合力
F=
| (Tcos53°)2+(T+Tsin53°)2 |
解答: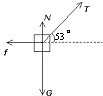 解:(1)物体受力如图,设地面对物体的弹力大小为N,地面对物体的摩擦力大小为f,由共点力平衡条件有
解:(1)物体受力如图,设地面对物体的弹力大小为N,地面对物体的摩擦力大小为f,由共点力平衡条件有
竖直方向 N+Tsin53°-mg=0
代入数据得 N=220N
水平方向 f=Tcos53°=60N
(2)左边绳子的拉力分解为水平向左的分力Tcos53?,竖直向下的分力Tsin53?,
故两根绳子对滑轮向下的拉力为(T+Tsin53?),
所以两根绳子对滑轮的作用力的合力F=
而滑轮对中轴的作用力等于两边绳子对滑轮的作用力,故滑轮对中轴的作用力大小为
F=
=60
N≈190N
答:(1)地面对物体的弹力大小为220N,地面对物体的摩擦力大小为60N.
(2)滑轮对中轴的作用力等于190N.
 解:(1)物体受力如图,设地面对物体的弹力大小为N,地面对物体的摩擦力大小为f,由共点力平衡条件有
解:(1)物体受力如图,设地面对物体的弹力大小为N,地面对物体的摩擦力大小为f,由共点力平衡条件有竖直方向 N+Tsin53°-mg=0
代入数据得 N=220N
水平方向 f=Tcos53°=60N
(2)左边绳子的拉力分解为水平向左的分力Tcos53?,竖直向下的分力Tsin53?,
故两根绳子对滑轮向下的拉力为(T+Tsin53?),
所以两根绳子对滑轮的作用力的合力F=
| (Tcos53°)2+(T+Tsin53°)2 |
而滑轮对中轴的作用力等于两边绳子对滑轮的作用力,故滑轮对中轴的作用力大小为
F=
| (Tcos53°)2+(T+Tsin53°)2 |
| 10 |
答:(1)地面对物体的弹力大小为220N,地面对物体的摩擦力大小为60N.
(2)滑轮对中轴的作用力等于190N.
点评:本题的难点是第二问,主要是应该明白轻滑轮对中轴的作用力即压力是由下边两段绳子拉力造成的,故应该等于下边两段绳子拉力的矢量和.而求两段绳子拉力的矢量和时可以先将左边绳子的拉力分解为水平方向的分力和竖直方向的分力,从而求出两根绳子对滑轮向下的拉力,再用勾股定理求解.这样可以不用余弦定理而减小了计算量,提高了计算速度.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
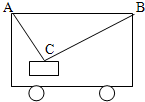 如图所示,物块的质量为m,车静止时绳AC、BC与水平方向的夹角分别为53°和37°,求:
如图所示,物块的质量为m,车静止时绳AC、BC与水平方向的夹角分别为53°和37°,求: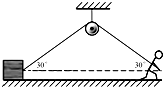 如图所示,物块的质量m=30kg,细绳一端与物块相连,另一端绕过光滑的轻质定滑轮,当人用100N的力斜向下拉绳子时,滑轮两侧细绳与水平方向的夹角均为30°,物体在水平面上保持静止,滑轮上端的悬绳竖直(取g=10m/s2).
如图所示,物块的质量m=30kg,细绳一端与物块相连,另一端绕过光滑的轻质定滑轮,当人用100N的力斜向下拉绳子时,滑轮两侧细绳与水平方向的夹角均为30°,物体在水平面上保持静止,滑轮上端的悬绳竖直(取g=10m/s2).
