题目内容
17.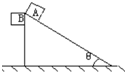 如图示,两物体A和B处于同一高度,其中mA=2mB,A沿固定在地面上的光滑斜面由静止开始下滑(斜面倾角θ=30°),B自由下落,最后到达同一水平面,则( )
如图示,两物体A和B处于同一高度,其中mA=2mB,A沿固定在地面上的光滑斜面由静止开始下滑(斜面倾角θ=30°),B自由下落,最后到达同一水平面,则( )| A. | 两物体的重力做功相同 | B. | 重力的平均功率相同 | ||
| C. | 到达底端时,重力的瞬时功率相同 | D. | 到达底端时,两物体的速率相同 |
分析 质量相同的两物体处于同一高度,A沿固定在地面上的光滑斜面下滑,而B自由下落,到达同一水平面.重力势能全转变为动能,重力的平均功率是由重力作功与时间的比值,而重力的瞬时功率则是重力与重力方向的速率乘积.
解答 解:A、两物体质量不同,初末位置的高度差h相同,重力做的功W=mgh不相同,故A错误;
B、B做自由落体运动,时间t=$\sqrt{\frac{2h}{g}}$,从A做匀加速直线运动,加速度a=$\frac{mgsin30°}{m}=\frac{1}{2}g$,则有:$\frac{h}{sin30°}=\frac{1}{2}a{{t}_{1}}^{2}$,解得:${t}_{1}=\sqrt{\frac{8h}{g}}$,则A重力平均功率$\overline{{P}_{A}}=\frac{{m}_{A}gh}{\sqrt{\frac{8h}{g}}}{=m}_{A}gh\sqrt{\frac{g}{8h}}$,
B重力平均功率$\overline{{P}_{B}}=\frac{{m}_{B}gh}{\sqrt{\frac{4h}{g}}}{=m}_{B}gh\sqrt{\frac{g}{4h}}$=$\frac{1}{2}{m}_{A}gh\sqrt{\frac{g}{4h}}$=${m}_{A}gh\sqrt{\frac{g}{16h}}$,故B错误;
D、根据动能定理可知mgh=$\frac{1}{2}m$v2,则到达底端的速率v=$\sqrt{2gh}$,相等,重力不相同,所以重力的瞬时功率不等,故C错误,D正确;
故选:D
点评 重力做功决定重力势能的变化与否,若做正功,则重力势能减少;若做负功,则重力势能增加.而重力的平均功率与瞬时功率的区别是:平均功率是做功与时间的比值,瞬时功率是力与速度在力的方向上的速度乘积.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )
如图所示,M是一小型理想变压器,接线柱a、b接在电压u=311sin 314t (V)的正弦交流电源上,变压器右侧部分为一火警报警系统原理图,其中R2是半导体热敏传感器(温度升高时R2的电阻减小),电流表A2安装在值班室,显示通过R1的电流,电压表V2显示加在报警器上的电压(报警器未画出),R3为一定值电阻.当传感器R2所在处出现火警时,以下说法中正确的是( )| A. | A1的示数增大,A2的示数减小 | B. | A1的示数不变,A2的示数增大 | ||
| C. | V1的示数减小,V2的示数减小 | D. | V1的示数增大,V2的示数增大 |

| A. | 线圈转动的转速为50r/s | B. | 0.01s时,线圈平面与磁感线平行 | ||
| C. | 0.15s时,电流表的示数为0A | D. | 0.02s时,E点电势高于F点电势 |
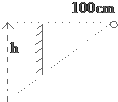 如图所示,在竖直放置的平面镜前100cm处,看见一个物体的像恰好全部映在平面镜内,已知平面镜自身的高度为12cm,镜内的像在镜后50cm处,则此物体的高度应为( )
如图所示,在竖直放置的平面镜前100cm处,看见一个物体的像恰好全部映在平面镜内,已知平面镜自身的高度为12cm,镜内的像在镜后50cm处,则此物体的高度应为( )| A. | 6cm | B. | 12cm | C. | 18cm | D. | 24cm |
| A. | 运动员对足球做的功为W1=mgh+$\frac{1}{2}$mv2-W2 | |
| B. | 足球机械能的变化量为W1-W2 | |
| C. | 足球克服阻力做的功为W2=mgh+$\frac{1}{2}$mv2-W1 | |
| D. | 运动员刚踢完球的瞬间,足球的动能为mgh+$\frac{1}{2}$mv2 |
| A. | 轨道半径约为卡戎的$\frac{1}{7}$ | B. | 角速度大小与卡戎的相同 | ||
| C. | 线速度大小约为卡戎的7倍 | D. | 向心力大小约为卡戎的7倍 |
 如图所示,一闭合直角三角形线框以速度v匀速穿过匀强磁场区域,从AC边进入磁场区开始计时,到B点离开磁场区的过程中,线框内感应电流的情况(以逆时针方向为电流的正方向)是( )
如图所示,一闭合直角三角形线框以速度v匀速穿过匀强磁场区域,从AC边进入磁场区开始计时,到B点离开磁场区的过程中,线框内感应电流的情况(以逆时针方向为电流的正方向)是( )






