题目内容
先后用相同材料制成的橡皮条彼此平行的沿水平方向拉同一质量为m的物块，且每根橡皮条的伸长量均相同，物块m在橡皮条拉力的作用下所产生的加速度a与所用橡皮条的数目n的关系如图所示．下列措施中能使图线的截距变化的是（ ）分析：对物体进行受力分析，根据牛顿第二定律求出加速度a与所用橡皮条的数目n的关系表达式，找出影响直线图线的纵截距的因数，再根据题目求解．
解答：解：设摩擦力为f，每条橡皮条的拉力为F，根据牛顿第二定律则有：
F合=nF-f=ma
a=
=
?n-
而摩擦力为f=μmg
则a=
?n-
=
?n-μg
所以在a-n的函数表达式中图线的纵截距是-μg，所以能使图线的纵截距改变的是物体与水平面的动摩擦因数．
故选：D．
F合=nF-f=ma
a=
| nF-f |
| m |
| F |
| m |
| f |
| m |
而摩擦力为f=μmg
则a=
| F |
| m |
| f |
| m |
| F |
| m |
所以在a-n的函数表达式中图线的纵截距是-μg，所以能使图线的纵截距改变的是物体与水平面的动摩擦因数．
故选：D．
点评：对该实验要明确实验原理，能够把物理规律和数学知识结合起来，知道纵截距的物理意义．
练习册系列答案
相关题目
先后用相同材料制成的橡皮条彼此平行地沿水平方向拉同一质量为m的物块，且每次使橡皮条的伸长量均相同，物块m在橡皮条的拉力作用下所产生的加速度a与所拉橡皮条的数目n的关系如图所示．若更换物块所在水平面的材料，在重复这个实验，则图中直线与水平轴间的夹角θ将（ ）
（2010?盐城一模）先后用相同材料制成的橡皮条彼此平行地沿水平方向拉同一质量为m的物块，且每根橡皮条的伸长量均相同，物块m在橡皮条拉力的作用下所产生的加速度a与所用橡皮条的数目n的关系如图所示．下列措施中能使图线的纵截距改变的是（ ）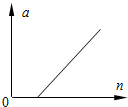
（2011?江苏模拟）先后用相同材料制成的橡皮条彼此平行地沿水平方向拉同一质量为m的物块，且每根橡皮条的伸长量均相同，物块在橡皮条拉力的作用下所产生的加速度a与所用橡皮条的数目n的关系如图所示．则（ ）