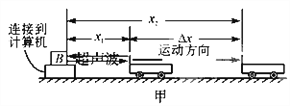
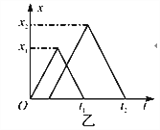
题目内容
【题目】如图甲所示,游乐场的过山车可以底朝上在竖直圆轨道上运行,可抽象为图乙所示的模型.倾角为45°的直轨道AB、半径R=10 m的光滑竖直圆轨道和倾角为37°的直轨道EF.分别通过水平光滑衔接轨道BC、C′E平滑连接,另有水平减速直轨道FG与EF平滑连接,EG间的水平距离l=40 m.现有质量m=500 kg的过山车,从高h=40 m处的A点静止下滑,经BCDC′EF最终停在G点.过山车与轨道AB、EF间的动摩擦因数均为μ1=0.2,与减速直轨道FG间的动摩擦因数μ2=0.75.过山车可视为质点,运动中不脱离轨道,g取10 m/s2.求:

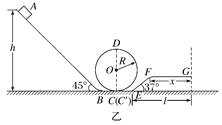
(1)过山车运动至圆轨道最低点C时的速度大小;
(2)过山车运动至圆轨道最高点D时对轨道的作用力;
(3)减速直轨道FG的长度x.(已知sin 37°=0.6,cos 37°=0.8)
【答案】(1)![]() (2)7×103 N (3)30 m
(2)7×103 N (3)30 m
【解析】试题分析:根据动能定理可求过山车运动至圆轨道最低点C时的速度大小;过山车从C到D的过程,由动能定理可得经过D点时的速度,由牛顿第二定律可求过山车运动至圆轨道最高点D时轨道对过山车的作用力,从而求得过山车运动对轨道的作用力。对C到G点的过程,运用动能定理,求出减速轨道FG的长度x.
(1)设C点的速度为vC,由动能定理得
![]()
代入数据解得: ![]()
(2)设D点速度为vD,从C到D由动能定理得
![]()
在D点,由牛顿第二定律得
![]()
解得:F=7×103 N
由牛顿第三定律知,过山车在D点对轨道的作用力为7×103 N,方向竖直向上.
(3) 对C到G点的过程全程应用动能定理:
![]()
代入数据解得:x=30m.

【题目】T27次列车是中国铁路运行于首都北京至西藏拉萨之间的特快旅客列车,自2006年7月1日起开行,为铁道部确定的青藏铁路运营初期开行的三对旅客列车之一,现由北京铁路局北京客运段京藏车队负责客运任务。设火车能在每个站都能准时到达,准点开出。请你根据列车时刻表,
站次 | 站名 | 到达时间 | 发车时间 | 停留 | 累计运行时间 | 里程(km) |
1 | 拉萨 | 始发站 | 13:48 | 0分 | 0 | 0 |
2 | 那曲 | 17:11 | 17:17 | 6分 | 3小时23分 | 322 |
3 | 格尔木 | 次日02:48 | 次日03:08 | 20分 | 13小时 | 1142 |
4 | 西宁西 | 次日12:00 | 次日12:20 | 20分 | 22小时12分 | 1960 |
5 | 兰州 | 次日14:55 | 次日15:10 | 15分 | 1天1小时7分 | 2188 |
6 | 中卫 | 次日20:10 | 次日20:19 | 9分 | 1天6小时22分 | 2494 |
7 | 太原 | 第3天03:17 | 第3天03:23 | 6分 | 1天13小时29分 | 3245 |
8 | 石家庄北 | 第3天05:36 | 第3天05:40 | 4分 | 1天15小时48分 | 3470 |
9 | 北京西 | 第3天08:19 | 终点站 | 0分 | 1天18小时31分 | 3761 |
(1)计算出火车由拉萨站开出直至到达那曲站,运行的平均速度是多少?
(2)计算出火车由太原站开出直至到达石家庄北站,运行的平均速度是多少?