题目内容
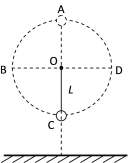
【题目】如图所示,一不可伸长的轻质细绳,绳长为L,一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气阻力)。
(1)若小球通过最高点A时的速度为v,求v的最小值和此时绳对小球拉力F的大小;
(2)若小球恰好通过最高点A且悬点距地面的高度h=2L,小球经过B点或D点时绳突然断开,求两种情况下小球从抛出到落地所用时间之差Δt;
(3)若小球运动到最低点C或最高点A时,绳突然断开,两种情况下小球从抛出到落地水平位移大小相等,则O点距离地面高度h与绳长L之间应满足怎样的关系?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 。
。
【解析】
(1)球通过最高点时的速度为v,根据牛顿第二定律有:
![]()
解得:
![]()
当拉力F为零时,速度v的最小值为![]()
(2)若小球恰好通过最高点![]() ,由机械能守恒
,由机械能守恒
![]()
解得:
![]()
从B点、D点小球分别竖直上抛和竖直下抛,则
![]()
(3)小球运动到最高点A绳断开后平抛运动,则
![]()
![]()
小球运动到最低点C绳断开后平抛运动,则
![]()
![]()
从A到C由机械能守恒定律得
![]()
又![]() ;
;
联立上述各式解得
![]()
小球圆周运动到最高点A时
![]()
解得![]() 。
。

练习册系列答案
相关题目