题目内容
【题目】如图所示为内壁光滑的固定半球面，球心为O，最低点为C，有两个可视为质点且质量相同的小球A和B，在球面内壁两个高度不同的水平面内做匀速圆周运动，A球的轨迹平面高于B球的轨迹平面，A、B两球与O点的连线与竖直线OC间的夹角分别为a=53°和β=37°，（sin 37°=0.6，cos 37°=0.8）;则 ( )
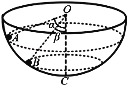
A. A、B两球所受支持力的大小之比为3:4
B. A、B两球运动的周期之比为2
:3
C. A、B两球的角速度之比为2
:3
D. A、B两球的线速度之比为8
:9
【答案】CD
【解析】由于小球在运动的过程中受到的合力沿水平方向，且恰好提供向心力，所以根据平行四边形定则得， 
，则
．故A错误．小球受到的合外力： 
，r=Rsinθ，解得
， 
．故B错误．根据公式：mgtanθ=mω2r，所以： 
，所以： 
．故C正确．据
得： 
所以： 
．故D正确；故选CD.
练习册系列答案
阅读快车系列答案
相关题目
