题目内容
9. 如图所示,AB是倾角为θ的光滑直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,求:
如图所示,AB是倾角为θ的光滑直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可视为质点)从直轨道上的P点由静止释放,结果它能在两轨道间做往返运动.已知P点与圆弧的圆心O等高,求:(1)物体做往返运动的过程中,通过B时的速度大小;
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力.
分析 (1)物体从P到B的过程,运用动能定理列式,可求得物体通过B时的速度大小.
(2)由动能定理求出物体通过最低点E时的速度,由牛顿运动定律求物体对轨道的压力.
解答 解:(1)物体从P到B的过程,由动能定理得
$mgRcosθ=\frac{1}{2}mυ_B^2$
可得 ${υ_B}=\sqrt{2gRcosθ}$
(2)从P到E的过程,由动能定理得
$mgR=\frac{1}{2}mυ_E^2$
得 ${υ_E}=\sqrt{2gR}$
在E点,由牛顿第二定律有
$N-mg=\frac{mυ_E^2}{R}$
可得 N=3mg
由牛顿第三定律可知:N′=N=3mg,方向竖直向下.
答:
(1)物体做往返运动的过程中,通过B时的速度大小为$\sqrt{2gRcosθ}$;
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力是3mg,方向竖直向下.
点评 本题是动能定理和向心力知识的综合应用,要明确它们之间的联系是速度,要注意分析物体的运动过程,灵活选取研究的过程,反复运用动能定理.

练习册系列答案
相关题目
17.比赛用的冰壶和冰球均以相同的初速度在水平冰面上滑行,已知两者与比冰面的动摩擦因数相同,则( )
| A. | 冰球的加速度大于冰壶的加速度 | B. | 冰球的加速度小于冰壶的加速度 | ||
| C. | 冰球的加速度等于冰壶的加速度 |
14.通过一个导体电流是2A,经过4min通过该导体横截面的电量是( )
| A. | 8C | B. | 20C | C. | 480C | D. | 1200C |
 如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历时间为t1,A、B两点间距离为d,缆绳质量忽略不计.求:
如图,用跨过光滑定滑轮的缆绳将海面上一艘失去动力的小船沿直线拖向岸边.已知拖动缆绳的电动机功率恒为P,小船的质量为m,小船受到的阻力大小恒为f,经过A点时的速度大小为v0,小船从A点沿直线加速运动到B点经历时间为t1,A、B两点间距离为d,缆绳质量忽略不计.求: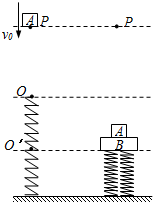 如图所示,轻弹簧一端固定在水平地面上,另一端点在O位置.质量为m=2kg的物块A(可视为质点)以初速度v0=$\sqrt{10}$m/s从弹簧正上方P点向下运动,与弹簧接触后压缩弹簧,将弹簧上端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0=0.8m,整个装置放在某种介质中,整个运动过程中物块受到的介质阻力为物块重力的0.25倍,弹簧均在弹性限度内,取g=10m/s2.求:
如图所示,轻弹簧一端固定在水平地面上,另一端点在O位置.质量为m=2kg的物块A(可视为质点)以初速度v0=$\sqrt{10}$m/s从弹簧正上方P点向下运动,与弹簧接触后压缩弹簧,将弹簧上端压到O′点位置后,A又被弹簧弹回.物块A离开弹簧后,恰好回到P点.已知OP的距离为x0=0.8m,整个装置放在某种介质中,整个运动过程中物块受到的介质阻力为物块重力的0.25倍,弹簧均在弹性限度内,取g=10m/s2.求: