题目内容
一质点作匀变速直线运动,第5s末速度为v,第9s末速度为-v,则质点在运动过程中( )
分析:根据匀变速直线运动的速度时间公式求出加速度,通过速度时间公式求出各个时刻的速度大小,通过匀变速直线运动的平均速度公式求出5s内和9s内的位移,从而比较大小.
解答:解:A、质点的加速度a=
=-
,则第7s末的速度v7=v+at=v+(-
)×2=0.故A正确.
B、第5s初的速度v4=v-at=v-(-
)×1=
,根据匀变速直线运动的平均速度公式得,第5s初到第9s末物体运动的平均速度
=
=
.故B错误.
C、第8s末的速度v8=v+at=v+(-
)×3=-
.故C错误.
D、质点的初速度v0=v-at=v-(-
)×5=
v,则5s内质点的位移x1=
×5=
,9s内的位移x2=
×9=
v,知5s内和9s内的位移相等.故D正确.
故选AD.
| -v-v |
| 4 |
| v |
| 2 |
| v |
| 2 |
B、第5s初的速度v4=v-at=v-(-
| v |
| 2 |
| 3v |
| 2 |
. |
| v |
| ||
| 2 |
| v |
| 4 |
C、第8s末的速度v8=v+at=v+(-
| v |
| 2 |
| v |
| 2 |
D、质点的初速度v0=v-at=v-(-
| v |
| 2 |
| 7 |
| 2 |
| ||
| 2 |
| 45v |
| 4 |
| ||
| 2 |
| 45 |
| 4 |
故选AD.
点评:解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目

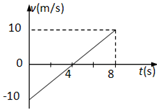 如图为一质点作匀变速直线运动的v-t图象,质点的质量为2kg,在前4s内向东运动由图线作出以下判断正确的是( )
如图为一质点作匀变速直线运动的v-t图象,质点的质量为2kg,在前4s内向东运动由图线作出以下判断正确的是( )