题目内容
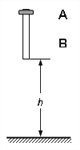
【题目】一圆环A套在一均匀圆木棒B上,A的高度相对B的长度来说可以忽略不计。A和B的质量都等于m,A和B之间的滑动摩擦力为f(f < mg)。开始时B竖直放置,下端离地面高度为h,A在B的顶端,如图所示。让它们由静止开始自由下落,当木棒与地面相碰后,木棒以竖直向上的速度反向运动。设碰撞时间很短,碰撞时原速率弹回,不考虑空气阻力。试求:
(1)木棒第二次着地时速度是多大?
(2)若在B再次着地前,要使A不脱离B,B至少应该多长?
【答案】(1)![]() ;(2)
;(2)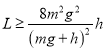 ;
;
【解析】(1)释放后A和B相对静止一起做自由落体运动,B着地前瞬间的速度
![]() ①
①
B与地面碰撞后,B竖直向上做匀减速运动。它的加速度大小为:
![]() ②
②
B与地面碰撞后向上运动到再次落回地面所需时间为![]() ③
③
取向下为正,B与地面碰后速度竖直向上,则
![]() ④
④
解出:v2=![]()
(2)B与地面碰后,A的加速度为![]() ⑤
⑤
此时间内A的位移![]() ⑥
⑥
要在B再次着地前A不脱离B,木棒长度L必须满足条件 L ≥ x ⑦
有以上方程联立解得 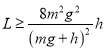

练习册系列答案
相关题目