��Ŀ����
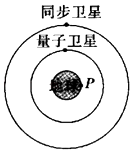
����Ŀ����ͼ��ʾ������ˮƽת̨�ϵ�С����A��B��C����ת̨һ���Խ��ٶȦ�����ת����ABC�������ֱ�Ϊ3m��2m��2m��A��B��B��ת̨��C��ת̨��Ķ�Ħ��������Ϊ�̣�BC��ת̨���ĵľ���ֱ�Ϊr��1.5r�������Ħ�������ڻ���Ħ����������˵����ȷ���ǣ� ��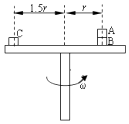
A.C��ת̨���Ħ������С����A��B���Ħ������С
B.B��A��Ħ������Сһ��Ϊ3��mg
C.����ת̨���ٶȦ�����A������������ˮƽת̨ת̨��
D.���ٶ�һ�����㣺�ء� ![]()
���𰸡�A,D
���������⣺A���������屣����Ծ�ֹ����ת̨һ��������Բ���˶�������Ħ�����ṩ���������� ![]() ��
�� ![]() ����֪C��ת̨���Ħ������С����A��B���Ħ������С����A��ȷ��
����֪C��ת̨���Ħ������С����A��B���Ħ������С����A��ȷ��
B��A��B���Ħ������һ���ﵽ���Ħ��������Ħ�����Ĵ�С��һ������3��mg����B����
C��D�����ݦ�mg=mR��2�ã��ٽ���ٶ� ![]() ��C�İ뾶����C�ȴﵽ���Ħ������ת̨�Ľ��ٶ�����
��C�İ뾶����C�ȴﵽ���Ħ������ת̨�Ľ��ٶ����� ![]() ��ͬʱ֪��C���ٽ���ٶ�С�������ٶ�����ʱ��C�ȴﵽ���Ħ������C��������ˮƽת̨����C����D��ȷ��
��ͬʱ֪��C���ٽ���ٶ�С�������ٶ�����ʱ��C�ȴﵽ���Ħ������C��������ˮƽת̨����C����D��ȷ��
��ѡ��AD
�������屣����Ծ�ֹ����ת̨һ��������Բ���˶�������Ħ�����ṩ������������ţ�ٵڶ����ɵó�Ħ�����Ĵ�С��ϵ���������Ħ�������������Ի������ٽ���ٶȣ��Ӷ������жϣ�

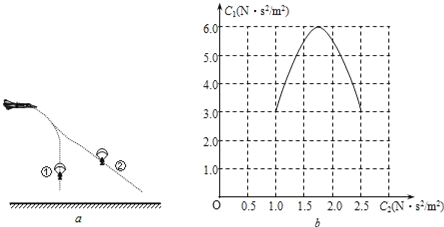
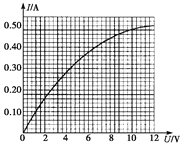
����Ŀ��Ϊ��֤���ܶ�����ijͬѧ���������ʵ�飮��һ��ֱľ��һ�˵�����һ�˲���װһ�ٶȴ���������С�����ɾ�ֹ��ľ��h�ߴ����Ӵ���������ƽ���������ɻ������ٶȴ�����ʱ���������龭�˴�ʱ���ٶ�v����ͼ��ʾ����θı们����»��߶�h��б�����Dz��䣩����Ӧ���ٶ�ֵ��¼�ڱ��У�
�»��߶�h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
�ٶ�v/ms��1 | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
Ҫ���ֱ�۵�˵���˹��̶��ܶ����Ƿ��������ͬѧ��������hΪ���������ϵ������Ϊ����ϵ�ĺ���Ӧ���� �� ��ʵ���Ƿ���Ҫƽ��Ħ��������ǡ�����