题目内容
18. 如图所示的四个定值电阻的阻值都是R,电键S闭合时,有一质量为m,电荷量为q的小球静止于平行板电容器极板间的中点O,现在把电键打开,此小球向一个极板运动,并与此极板相碰,碰撞时无机械能损失,碰撞后小球恰能运动到另一极板处,设两极板间的距离为d,电源内电阻不计,试计算:
如图所示的四个定值电阻的阻值都是R,电键S闭合时,有一质量为m,电荷量为q的小球静止于平行板电容器极板间的中点O,现在把电键打开,此小球向一个极板运动,并与此极板相碰,碰撞时无机械能损失,碰撞后小球恰能运动到另一极板处,设两极板间的距离为d,电源内电阻不计,试计算:(1)电源电动势E;
(2)小球和电容器一个极板碰撞后所带电荷量q′.
分析 (1)电键S闭合时,根据串并联电路的特点,求出电容器板间电压与电动势的关系,对小球受力情况进行分析,由电场力与重力平衡,即可求出板间电压,解得电源的电动势.
(2)断开S,由电路的关系求出电容器的板间电压,对带电小球运动的全过程,根据动能定理求解小球与极板碰撞后所带的电荷量.
解答 解:(1)电键K闭合时,R1和R3的并联电阻为R13=0.5R
总电阻为:R总=R4+R13=1.5R,
总电流为:I=$\frac{E}{1.5R}$
R4两端电压为 U4=IR=$\frac{2}{3}$E,即为电容器两端的电压.小球静止,即电场力与重力平衡,有:
qE电=mg
又有 U4=E电d,可得电源电动势为:
E=$\frac{3mgd}{2q}$
(2)电键K打开时,R4两端电压为:
U′4=$\frac{1}{2}$E
平行板电容器间的电场强度变为:E′电=$\frac{U{′}_{4}}{d}$=$\frac{3mg}{4q}$
小球所受电场力变为:F′=qE′电=$\frac{3}{4}$mg<mg
所以小球向下加速运动,根据牛顿第二定律得:
mg-F′=ma
解得:a=$\frac{g}{4}$
小球到达下极板时的速度为:v1=$\sqrt{2a•\frac{d}{2}}$=$\frac{1}{2}\sqrt{gd}$
碰撞没有机械能损失,返回时有:v2=$\frac{1}{2}\sqrt{gd}$
向上运动由动能定律有:-mgd+q′U4′=0-$\frac{1}{2}$mv22;
解得:q′=$\frac{7}{6}$q
答:(1)电源电动势为$\frac{3mgd}{2q}$.
(2)小球和极板碰撞后的带电量为$\frac{7}{6}q$.
点评 本题是电路与电场两部分知识的综合,关键是确定电容器的电压与电动势的关系.

 习题精选系列答案
习题精选系列答案| A. | 小球过最高点时,杆的弹力不可以等于零 | |
| B. | 小球过最高点时的最小速度为$\sqrt{gl}$ | |
| C. | 小球到最高点时速度v>0,小球一定能通过最高点做圆周运动 | |
| D. | 小球过最高点时,杆对球的作用力可以与小球所受重力方向相反 |
 如图所示,物体在水平力F作用下静止在斜面上,若稍增大水平力F,而物体仍能保持静止,下列说法正确的是( )
如图所示,物体在水平力F作用下静止在斜面上,若稍增大水平力F,而物体仍能保持静止,下列说法正确的是( )| A. | 斜面对物体的静摩擦力及支持力都不一定增大 | |
| B. | 斜面对物体的静摩擦力及支持力都一定增大 | |
| C. | 斜面对物体的静摩擦力一定增大,支持力不一定增大 | |
| D. | 斜面对物体的静摩擦力不一定增大,支持力一定增大 |
 如图所示,矩形线圈有N匝,面积大小为S,放在水平面内,加一个竖直向下的范围较大的匀强磁场,磁感应强度为B,则穿过平面的磁通量是多少?若使线圈绕ab边转过60°,则穿过线圈平面的磁通量是多少?
如图所示,矩形线圈有N匝,面积大小为S,放在水平面内,加一个竖直向下的范围较大的匀强磁场,磁感应强度为B,则穿过平面的磁通量是多少?若使线圈绕ab边转过60°,则穿过线圈平面的磁通量是多少?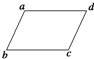 如图所示,匀强电场中有一平行四边形abcd,且平行四边形所在平面与场强方向平行.其中φa=10V,φb=6V,φd=8V,则c点电势为4V.
如图所示,匀强电场中有一平行四边形abcd,且平行四边形所在平面与场强方向平行.其中φa=10V,φb=6V,φd=8V,则c点电势为4V. 如图所示,一个放在水平面上的静止的物体,受到与水平方向成37°角斜向上方的拉力F1=10N,在水平地面上向前移动距离s=2m,物体与地面间的滑动摩擦力F2=3.2N,求外力对物体所做的总功.(sin37°=0.6,cos37°=0.8)
如图所示,一个放在水平面上的静止的物体,受到与水平方向成37°角斜向上方的拉力F1=10N,在水平地面上向前移动距离s=2m,物体与地面间的滑动摩擦力F2=3.2N,求外力对物体所做的总功.(sin37°=0.6,cos37°=0.8)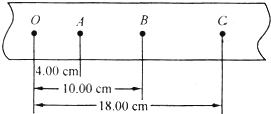 小华做“研究匀变速直线运动”的实验中,打点计时器使用交流电源的频率为50Hz,纸带记录了小车运动的情况.
小华做“研究匀变速直线运动”的实验中,打点计时器使用交流电源的频率为50Hz,纸带记录了小车运动的情况.