题目内容
如图,两光滑导体框ABCD与EFGH固定在水平面内,在D点平滑接触,A、C分别处于FE、HG的沿长线上,ABCD是边长为a的正方形;磁感强度为B的匀强磁场竖直向上;导体棒MN置于导体框上与导体框良好接触,以速度v沿BD方向从B点开始匀速运动,已知线框ABCD及棒MN单位长度的电阻为r,线框EFGH电阻不计。求:
⑴导体棒MN在线框ABCD上运动时,通过MN电流的最大值与最小值;
⑵为维持MN在线框ABCD上的匀速运动,必须给MN施加一水平外力,用F(t)函数表示该力;
⑶导体棒达D点时立即撤去外力,则它还能前进多远(设EF、GH足够长)?
⑴导体棒MN在线框ABCD上运动时,通过MN电流的最大值与最小值;
⑵为维持MN在线框ABCD上的匀速运动,必须给MN施加一水平外力,用F(t)函数表示该力;
⑶导体棒达D点时立即撤去外力,则它还能前进多远(设EF、GH足够长)?

⑴
⑵

⑵

⑴设某时刻棒MN交线框于P、S点,令PS长为l,则
此时电动势E = Blv
MN左侧电阻 MN右侧电阻
MN右侧电阻
则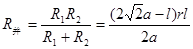
故:I= ……………………………………………④
……………………………………………④
因导线框ABCD关于AC对称,所以通MN的电流大小也具有对称性,所以
当l = 0时,电流最小值
当l = 时,电流最大值
时,电流最大值
⑵设MN到达B的时间为t0,则t0= ,到达D点用时2t0,
,到达D点用时2t0,
当0≤t≤t0时,由④式得: (其中vt ="l" )
(其中vt ="l" )
代入F=BIl得:F =
当t0≤t≤2t0时,将 代入④式得:
代入④式得:
代入F=BIl得:
⑶导线框进入矩形磁场后,由牛顿第二定律得:

 取任意△t时间有:
取任意△t时间有:




此时电动势E = Blv
MN左侧电阻
 MN右侧电阻
MN右侧电阻
则
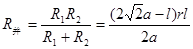
故:I=
 ……………………………………………④
……………………………………………④因导线框ABCD关于AC对称,所以通MN的电流大小也具有对称性,所以
当l = 0时,电流最小值

当l =
 时,电流最大值
时,电流最大值
⑵设MN到达B的时间为t0,则t0=
 ,到达D点用时2t0,
,到达D点用时2t0,当0≤t≤t0时,由④式得:
 (其中vt ="l" )
(其中vt ="l" )代入F=BIl得:F =

当t0≤t≤2t0时,将
 代入④式得:
代入④式得:
代入F=BIl得:

⑶导线框进入矩形磁场后,由牛顿第二定律得:

 取任意△t时间有:
取任意△t时间有:





练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 =
=




 倍
倍


 ,现将它们以相同的速度v从右图中所示位置,由匀强磁场B1拉进另一匀强磁场B2中,(已知两磁场方向均垂直于纸面向里,且B1 <B2),在此过程中两个线框中通过导线某一横截面的电量之比
,现将它们以相同的速度v从右图中所示位置,由匀强磁场B1拉进另一匀强磁场B2中,(已知两磁场方向均垂直于纸面向里,且B1 <B2),在此过程中两个线框中通过导线某一横截面的电量之比 。
。