题目内容

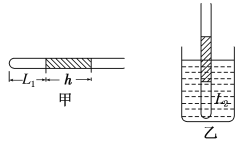
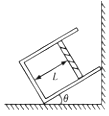
【题目】某实验小组利用如图甲所示的实验装置探究合力做功与速度变化的关系。在粗糙程度相同的斜面上依次标记间隔相等的O、A、B、C、D、E共6条刻线，两相邻刻线间的距离均为L，在O点固定一个光电门，光电门和数字计时器相连（图中未画出），小车上固定有宽度为d的遮光片。实验中，分别从A、B、C、D、E无初速度释放小车，分别测出小车经过光电门时的时间，通过计算合力做的功和小车经过光电门时的速度，找到两者之间的关系。（空气阻力忽略不计）

（1）若小车从A到O合力做的功为W，则小车从E到O合力做的功为_________。

（2）某次实验时，数字计时器记录的时间为△t，则小车经过光电门所在位置的速度为______。

（3）该实验小组得到v2与x（x为小车释放点到光电门的距离）的图象如图乙所示，斜率为k，若该实验小组用天平测出小车质量为m。根据图象可以得出的是（）

A．小车所受的阻力

B．小车运动的加速度

C．小车所受的合力

D．从释放点到光电门合力做功

【答案】5W ； BCD

【解析】

（1）小车在同一个斜面上下滑，合力大小恒定，经过相同位移做的功相等，若小车从A到O合力做的功为W，则小车从E到O合力做的功为5W；

（2）因为遮光片非常窄，所以通过遮光片的平均速度，可近似认为通过该点的平均速度，故有；

（3）根据公式可得，图像的斜率，故可求解出小车运动的加速度，根据牛顿第二定律可求解小车所受的合力，BC正确；由于不知道斜面的夹角，所以无法求解小车所受阻力，A错误；根据动能定理可得，D正确．

练习册系列答案
相关题目

【题目】如图所示，在平面直角坐标系中存在有界匀强电场区域，电场方向沿y轴负方向，电场强度大小为E.边界为y轴，右边界为平行于y轴的虚线，右边界与x轴交点横坐标等于L（L>0）。一带电粒子（不计重力）从坐标原点O处以初速度v0沿x轴正方向射入电场区域，粒子所带电荷量等于-q，质量为m。求：

（1）带电粒子从电场右边界射出时的速度v的大小；

（2）若电场方向在平面内沿逆时针方向旋转θ（θ<90°)角，恰好使粒子不射出电场右边界，sinθ的值是多少。

【题目】某学习小组为了验证碰擅中的动量守恒，设计了如下方案：如图所示，斜面与水平桌面平滑连接，先將质量为M的滑块A从斜面上某位置由静止释放，测量出滑块在水平桌面滑行的距离；接着将质量为m、相同材料的小滑块B放在斜面底端的水平轨道上，再让A从斜面上同一位置由静止释放，A与B碰撞后，测量出各自沿桌面滑行的距离、.实验中M>m，重力加速度为g。

(1)若满足关系式____________________，则验证了A和B的碰撞动量守恒(用题目中给出的物理量表示).

(2)若满足关系式___________________，则验证了A 和B的碰撞是弹性碰擅(用题目中给出的物理量表示)。

(3)若桌面稍有倾斜，本实验_________(填正确选项)。

A.无法验证动量守恒

B.仍可以验证动量守恒

C.满足动量守恒的关系式将改变

【题目】如图所示，在一端开口、一端封闭粗细均匀的玻璃管内，一段长为h＝25 cm的水银柱封闭着一定质量的理想气体，当玻璃管水平放置时，管内封闭的气柱长度为L1＝20 cm(如图甲)，这时的大气压强p0＝75 cmHg，室温是t1＝27 ℃。将玻璃管缓慢地转过90°，使它开口向上，并竖直浸入热水中(如图乙)，待稳定后，测得玻璃管内气柱的长度L2＝17.5 cm。

(i)求此时管内气体的温度t2；

(ii)保持管内气体的温度t2不变，往玻璃管内缓慢加入水银，当封闭的气柱长度L3＝14 cm时，加入的水银柱长度Δh是多少(玻璃管足够长)。

【题目】如图所示，质量M=2kg的物块A放在水平地面上，滑轮固定在天花板上，细绳跨过滑轮，一端与物块A连接，另一端悬挂质量m=1kg的物块B，细绳竖直，A、B处于静止状态。现对物体A施加向左的水平外力F，使A沿水平面向左缓慢移动。物块A刚开始移动时水平外力F1＝3N，不计绳与滑轮间的摩擦，重力加速度g取10 m/s2，最大静摩擦力等于滑动摩擦力，求：

(1)物块A与水平地面间的动摩擦因数μ；

(2)当连接物块A的细绳与竖直方向的夹角β=37°时，水平外力F2的大小。(已知sin37°=0.6，cos37°=0.8)

【题目】如图所示，一定质量的理想气体被光滑的活塞封闭在导热良好的气缸内．活塞质量为m＝20kg，横截面积为S＝0．01m2．气缸与水平面成＝30°角靠在墙上，活塞静止时，活塞下表面与气缸底部的距离L＝48cm，此时气体的温度为27℃．已知外界大气压强p0＝1．0X105Pa，并始终保持不变，重力加速度g＝10m／s2．求：

(1)若将气缸缓慢地沿逆时针方向转到竖直位置，此时活塞下表面与气缸底部的距离；

(2)若将缸内气体的温度升高，为使活塞仍处于第（1）问的位置不变，可在活塞上表面均匀添放铁沙，当缸内温度为47℃时，添加在活塞上表面的铁沙质量是多少？

【题目】如图所示，平行板电容器充电后，在其正中P点处有一个带电微粒恰好能保持静止状态。用什么方法能使该带电微粒仍在原处保持静止，且电势能增加（ ）

A. K闭合,将上极板M 接地，下移N

B. K闭合,将下极板N 接地，左移M

C. K断开,将下极板N 接地，上移N

D. K断开,将上极板M 接地，下移M

【题目】如图所示，一长为2d、宽为d、质量为m、阻值为r的矩形导线框放在具有理想边界的匀强磁场上方，已知虚线1、2之间的磁场方向垂直纸面向外，虚线2、3之间的磁场方向垂直纸面向里，且磁感应强度的大小均为B。现将导线框无初速度地释放，导线框的AB边到达虚线1位置时刚好匀速，当导线框的AB边到达虚线2、3之间时再次匀速。假设整个过程中导线框的AB边始终与虚线平行，忽略空气的阻力，重力加速度为g。则下列说法正确的是

A. 导线框从进入磁场到完全离开的整个过程中，安培力的大小恒定

B. 从导线框的AB边与虚线1重合到导线框的AB边刚到虚线2的过程中，导线框中产生的热量为2mgd

C. 导线框释放瞬间，AB边与虚线1的间距为

D. 当AB边运动到虚线2、3之间再次匀速时，导线框的速度大小为

【题目】关于自由落体运动，下列说法中不正确的是

A. 由静止释放且只受重力作用的物体所做的运动是自由落体运动

B. 自由落体运动是初速为零的匀加速直线运动

C. 自由落体运动在第1 s、第2s、第3s内的位移之比是1∶3∶5

D. 自由落体运动在第1 s、第2s、第3s内的位移之比是1∶4∶9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网