题目内容
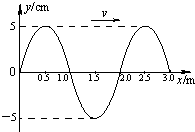 一列沿x轴正方向传播的简谐横波在t=0时刻的波形图如图所示,已知波速v=2m/s,试回答下列问题:
一列沿x轴正方向传播的简谐横波在t=0时刻的波形图如图所示,已知波速v=2m/s,试回答下列问题:(1)求x=2.5m处质点在0~4.5s内通过的路程及t=4.5s时的位移;
(2)写出x=2.0m处质点的振动函数表达式.
分析:(1)通过图象得出波长、振幅,根据波速和波长求出周期,利用一个周期的路程为4A和质点的振动情况求位移.
(2)利用波形平移判断x=2.0m质点的振动情况,再利用波传播的特点写出其振动函数表达式.
(2)利用波形平移判断x=2.0m质点的振动情况,再利用波传播的特点写出其振动函数表达式.
解答:解:(1)据图象知:波长λ=2m,A=5cm
由波速公式得:T=
=
s=1s
所以4.5s=4T+
即4.5s内路程:S=16A+2A=90cm
在t=4.5s 4T+
的位移:y=-5cm
(2)由上知振幅A=5cm,T=1s
所以ω=
=2πrad/s
据波的传播方向和波形平移可知,x=2.0m处质点将从平衡位置向下振动
所以y=-5sin2πt(cm)
答:(1)求x=2.5m处质点在0~4.5s内通过的路程为90cm及t=4.5s时的位移为-5cm;
(2)写出x=2.0m处质点的振动函数表达式y=-5sin2πt(cm).
由波速公式得:T=
| λ |
| v |
| 2 |
| 2 |
所以4.5s=4T+
| T |
| 2 |
即4.5s内路程:S=16A+2A=90cm
在t=4.5s 4T+
| T |
| 2 |
(2)由上知振幅A=5cm,T=1s
所以ω=
| 2π |
| T |
据波的传播方向和波形平移可知,x=2.0m处质点将从平衡位置向下振动
所以y=-5sin2πt(cm)
答:(1)求x=2.5m处质点在0~4.5s内通过的路程为90cm及t=4.5s时的位移为-5cm;
(2)写出x=2.0m处质点的振动函数表达式y=-5sin2πt(cm).
点评:解决本题的关键知道波速、波长、周期以及圆频率的关系,知道波的周期性,以及知道质点在一个周期内的路程等于4倍的振幅.

练习册系列答案
相关题目
 (2006?重庆)如图为一列沿x轴正方向传播的简谐横波在t=0时的波形.当R点在t=0时的振动状态传到S点时,PR范围内(含P、R)有一些质点正在向y轴负方向运动,这些质点的x坐标取值范围是( )
(2006?重庆)如图为一列沿x轴正方向传播的简谐横波在t=0时的波形.当R点在t=0时的振动状态传到S点时,PR范围内(含P、R)有一些质点正在向y轴负方向运动,这些质点的x坐标取值范围是( ) 一列沿x轴正方向传播的简谐横波,在t=0时刻波刚好传播到x=6m处的A点,如图所示,已知波的传播速度为48m/s.请回答下列问题:
一列沿x轴正方向传播的简谐横波,在t=0时刻波刚好传播到x=6m处的A点,如图所示,已知波的传播速度为48m/s.请回答下列问题: (2008?汝城县模拟)在坐标原点的波源 S产生一列沿x轴正方向传播的简谐横波,波速 v=400m/s,已知 t=0时,波刚好传播到 x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是 ( )
(2008?汝城县模拟)在坐标原点的波源 S产生一列沿x轴正方向传播的简谐横波,波速 v=400m/s,已知 t=0时,波刚好传播到 x=40m处,如图所示.在x=400m处有一接收器(图中未画出),则下列说法正确的是 ( )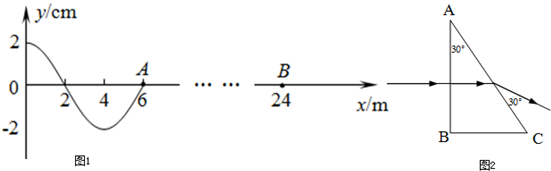
 如图所示,一列沿x轴正方向传播的简谐波在某时刻的波形图,其波速为20m/s,则下列说法正确的是( )
如图所示,一列沿x轴正方向传播的简谐波在某时刻的波形图,其波速为20m/s,则下列说法正确的是( )