题目内容
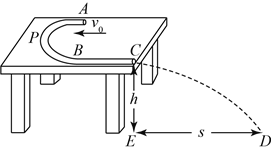
【题目】如图所示，长
、高
、质量
的长方体木箱在水平面上向右做直线运动．当木箱的速度
时，对木箱施加一个方向水平向左的恒力
，并同时将一个质量
的小球轻放在距木箱右端
处的
点（小球可视为质点，放在
点时相对于地面的速度为零），经过一段时间，小球脱离木箱落到地面．已知木箱与地面的动摩擦因数
，而小球与木箱之间的摩擦不计．取
，求：
（
）小球从开始离开木箱至落到地面所用的时间．
（
）小球放上
点后，木箱向右运动的最大位移．
（
）小球离开木箱时木箱的速度．
【答案】（
）
．
（
）
．
（
）
．
【解析】（
）木箱上表面的摩擦不计，因此小球在离开木箱前相对地面处于静止状态，离开木箱后将作自由落体运动，则小球落到地面所用的时间为：
，即： 
；
（
）小球放上木箱后相对地面静止，以木箱为研究对象，由牛顿第二定律：
代入数据计得出木箱的加速度： 
．
木箱向右运动的最大位移： 
；
（
）因为
，故木箱在向右运动期间，小球不会从木箱的左端掉下，木箱向左运动时，根据牛顿第二定律得
计算得出木箱向左运动的加速度
．
设木箱向左运动的位移为
时，小球从木箱的右端掉下，则：
．由
得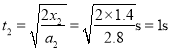
故小球刚离开木箱时的速度： 
，方向向左。
练习册系列答案
相关题目
