题目内容
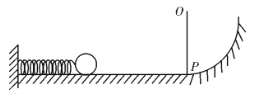
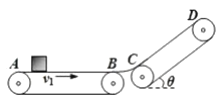
【题目】如图所示,半径为R=1.5m的光滑员弧支架竖直放置,圆心角θ=60°,支架的底部CD离地面足够高,圆心O在C点的正上方,右侧边缘P点固定一个光滑小轮,可视为质点的小球A、B分别系在足够长的跨过小轮的轻绳两端,两球的质量分别为mA=0.3kg、mB=0.1kg。将A球从紧靠小轮P处由静止释放,若A球运动到C点时刻,轻绳突然断裂,g=10m/s2,求:
(1)在轻绳断裂瞬间,A球对圆弧轨道的压力为多大;
(2)从轻绳断裂瞬间开始,经过多长时间两球重力功率的大小相等?(计算结果可用根式表示)
【答案】(1)3.8N;(2)![]() 。
。
【解析】
(1)A、B组成的系统机械能守恒
![]()
根据几何关系有
![]()
![]()
联立解得
![]()
联立解得
![]()
对A受力分析,应用向心力公式有
![]()
解得
![]()
由牛顿第三定律可知,A对圆弧轨道的压力大小为3.8N
(2)轻绳断裂后,A球做平抛运动,B球做竖直上抛运动,B球上抛初速度
![]()
设经过时间t两球重力功率的大小相等,则
![]()
根据速度时间公式有
![]()
![]()
联立解得
![]()

练习册系列答案
相关题目
【题目】为验证动能定理,某同学设计了如下实验。将一长直木板一端垫起,另一端侧面装一速度传感器,让小滑块由静止从木板h高处(从速度传感器所在平面算起)自由下滑至速度传感器时,读出滑块经此处时的速度v,如图所示。多次改变滑块的下滑高度h(斜面的倾角不变),对应的速度值记录在表中:
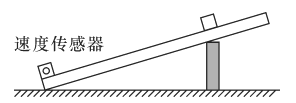
下滑高度h/m | 0.10 | 0.20 | 0.30 | 0.40 | 0.50 |
速度v/(m·s-1) | 0.633 | 0.895 | 1.100 | 1.265 | 1.414 |
要最简单直观地说明此过程动能定理是否成立,该同学建立了以h为纵轴的坐标系,你认为坐标系的横轴应该是___________,本实验是否需要平衡摩擦力___________(填“是”或“否”)。