��Ŀ����
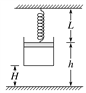
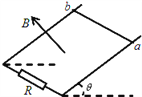
����Ŀ����ͼ��ʾ��������ǿ�ų��е������㹻�������費�Ƶ�ƽ�н����������L=1m������ƽ����ˮƽ��ɦ�=37��ǣ��¶�������ֵΪR�ĵ��裮��ǿ�ų�����ֱ�ڵ���ƽ�����ϣ��Ÿ�Ӧǿ��ΪB=0.4T������Ϊ0.2kg�����費�ƵĽ����������������ϣ����뵼�촹ֱ�ұ������ýӴ������Ǽ�Ķ�Ħ������Ϊ��=0.25���������ص����ɾ�ֹ��ʼ�»������������»��ٶȴﵽ�ȶ�ʱ���ٶȴ�СΪ10m/s��(ȡg=10m/s2��sin37��=0.6��cos37��=0.8)����
(1)�������ص��쿪ʼ�»�ʱ�ļ��ٶȴ�С��
(2)���������»��ٶȴﵽ�ȶ�ʱ����R���ĵĹ��ʣ�
(3)����R����ֵ��
���𰸡���1��4m/s2 ��2��8W ��3��2��
������������������������ʼ���»��������У��ܵ������������֧�����ͻ���Ħ��������ţ�ٵڶ���������ٶȣ�������������˶�ʱ���ٶ������ƽ�������Ͱ�������ʽ������ٶȣ�����������ʣ�����ȶ�ʱ��·�еĵ���������![]() �����衣
�����衣
��������ʼ�»��ij���Ϊ�㣬����ţ�ٵڶ�����
mgsin��-��mgcos��=ma
�������ݽ�ã�a =4m/s2
��2����������˶��ﵽ�ȶ�ʱ�����ٶ�Ϊv�����ܰ�����ΪF�����ص��췽������ƽ�⣬��������ƽ������mgsin��-��mgcos��=F
����ʽ���뼴��F=0.8N
��ʱ�������˷������������Ĺ��ʵ��ڵ�·�е���R���ĵĵ繦��
P=Fv
�������ݽ�ã�P=8W��
��3�����·�е���ΪI����Ӧ�綯��ΪE
E=BLv=0.4��1��10V=4V
����P=UI�ɵã� ![]()
�ɵ���![]()