Question

【题目】如图所示,竖直平面内有一光滑直杆AB,直杆AB长为L,杆与水平方向的夹角为θ(0°≤θ≤90°)，一质量为m的小圆环套在直杆上,给小圆环施加一与该竖直平面平行的水平向右的恒力F,并从A端由静止释放,现改变直杆和水平方向的夹角θ,已知F=2mg,重力加速度为g,则下列说法正确的是( )

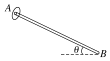
A. 当θ=30°时,小圆环在直杆上运动的时间最短

B. 当小圆环在直杆上运动的时间最短时,小圆环与直杆间一定有挤压

C. 当小圆环在直杆上运动的时间最短时,直杆与水平方向的夹角θ满足

D. 当小圆环在直杆上运动的时间最短时,小圆环的加速度为g

Answer 1

【答案】CD

【解析】

根据题意，结合牛顿第二定律，可知，力与重力的合力方向一定沿杆的方向，再依据矢量的合成法则，及三角知识，即可求解。

根据题意，小圆环在直杆上运动的时间最短，则加速度最大，即力与重力的合力方向沿杆的方向，此时小圆环与直杆间一定恰好没有挤压，如图所示：

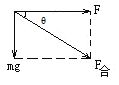
由几何关系有：，对应的夹角不等于；而此时合力，故加速度为，故AB错误，CD正确。故选CD。