题目内容
15. 如图所示,长1米的轻杆BO一端通过光滑铰链铰在竖直墙上,另一端装一轻小光滑滑轮,重力G=10N的物体通过摆线经滑轮系于墙上A点,平衡时OA恰好水平,现将A点沿着竖直墙向上缓慢移动少许,重新平衡后轻杆受到的压力恰好也为10牛,该过程中,外力所做的功至少为(小数点后保留两位)( )
如图所示,长1米的轻杆BO一端通过光滑铰链铰在竖直墙上,另一端装一轻小光滑滑轮,重力G=10N的物体通过摆线经滑轮系于墙上A点,平衡时OA恰好水平,现将A点沿着竖直墙向上缓慢移动少许,重新平衡后轻杆受到的压力恰好也为10牛,该过程中,外力所做的功至少为(小数点后保留两位)( )| A. | 0.86焦 | B. | 1.59焦 | C. | 2.07焦 | D. | 2.93焦 |
分析 本题可以以轻杆BO的O端上的滑轮为参照物,分析判断出滑轮竖直高度和OA绳子的长度的变化,即为知道物体提升的高度,再根据W=Gh计算即可.
解答  解:由于轻杆的重力不计,且杆两端是铰链光滑,滑轮也光滑,所以轻杆在O点处的作用力方向必沿杆,所以A点缓慢移动过程中,杆会平分两侧绳子间的夹角.
解:由于轻杆的重力不计,且杆两端是铰链光滑,滑轮也光滑,所以轻杆在O点处的作用力方向必沿杆,所以A点缓慢移动过程中,杆会平分两侧绳子间的夹角.
开始时,AO绳子水平,由于各段绳子的拉力大小等于物体重力的大小,所以可知此时杆与竖直方向的夹角为45°,这时杆中的弹力大小等于滑轮两侧绳子拉力的合力.
当将A点沿竖直方向向上缓慢移动一段距离后,重新达到平衡,由于这时杆受到的压力大小等于10N(等于物体的重力),说明这时两段绳子的夹角为120°.则杆与竖直方向的夹角为60°.
设杆的长度为L.
状态1时,AO绳子长度是 L1=Lsin45°=$\frac{\sqrt{2}}{2}$L
滑轮O点到B点的竖直方向距离为 h1=Lcos45°=$\frac{\sqrt{2}}{2}$L
状态2,杆与竖直方向夹角为60°,杆与此时的AO绳的夹角也是60°(∠AOB=60°),即这时三角形AOB是等边三角形,则这时AO段绳子的长度是 L2=L
可见,后面状态与原来状态相比,物体的位置提高的竖直高度为
h=(h2-h1)+(L2-L1)=($\frac{1}{2}$L-$\frac{\sqrt{2}}{2}$L)+(L-$\frac{\sqrt{2}}{2}$L)=($\frac{3}{2}-\sqrt{2}$)L
在该过程中,外力做的功等于整个系统增加的机械能.
所以所做的功是 W外=Gh=G($\frac{3}{2}-\sqrt{2}$)L=10×($\frac{3}{2}-\sqrt{2}$)×1J=≈0.86J
故选:A
点评 本题考查功的计算,但不能直接利用W=Fs计算,需要转化为克服重力做功的计算,关键要确定两个状态位置的关系,得出物体上升的高度.

 巧学巧练系列答案
巧学巧练系列答案| A. | 法拉第发现了电磁感应现象 | |
| B. | 惯性是物体的固有属性,速度大的物体惯性一定大 | |
| C. | 牛顿最早通过理想斜面实验得出力不是维持物体运动的必然结果 | |
| D. | 法拉第在实验中观察到电流的磁效应 |
| A. |  6V 0.65A | B. |  220V 0.68A | C. |  220V 1.60A | D. |  12V 4.58A |

| A. | 0-5s内的位移为10m | B. | 0-2s内的加速度为1m/s2 | ||
| C. | 第1s末与第4.5s末加速度方向相同 | D. | 第1s末与第3s末的速度方向相同 |
 如图所示的两种电路中,电源相同,各电阻阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3、A4读出的电流值分别为I1、I2、I3、I4,下列关系式中正确的是( )
如图所示的两种电路中,电源相同,各电阻阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3、A4读出的电流值分别为I1、I2、I3、I4,下列关系式中正确的是( )| A. | I2=2I1 | B. | I1<I4 | C. | I1<I2 | D. | I2<I3+I4 |

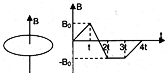 如图所示,一闭合圆形线圈水平放置,穿过它的竖直方向的匀强磁场磁感应强度随时间变化规律如图所示,规定B的方向以向上为正方向,感应电流以俯视顺时针的方向为正方向,在0-4t时间内感应电流随时间变化图象中正确的是( )
如图所示,一闭合圆形线圈水平放置,穿过它的竖直方向的匀强磁场磁感应强度随时间变化规律如图所示,规定B的方向以向上为正方向,感应电流以俯视顺时针的方向为正方向,在0-4t时间内感应电流随时间变化图象中正确的是( )




