题目内容
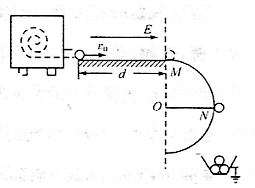
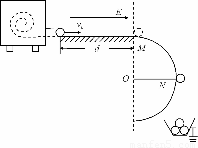
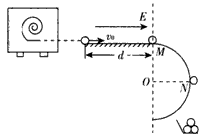
某塑料球成型机工作时，可以喷出速度v0=10m/s的塑料小球，已知喷出小球的质量m=1.0×10-4 kg，并且在喷出时已带了q=1.0×10-4 C的负电荷，如图所示，小球从喷口飞出后，先滑过长d=1.5m的水平光滑的绝缘轨道，而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道．今在水平轨道上加上水平向右的电场强度为E的匀强电场，小球将恰好从圆弧轨道的最高点M处水平飞出；若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后，小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内，g=10m/s2，求：
（1）所加电场的电场强度E；
（2）所加磁场的磁感应强度B．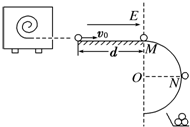
（1）所加电场的电场强度E；
（2）所加磁场的磁感应强度B．
（1）设小球在M点的速率为v1，只加电场时对小球在M点，根据牛顿第二定律有：
mg=m
在水平轨道上，对小球运用动能定理得：
qEd=
mv12-
mv02
联立两式解得：E=32V/m．
故所加电场的电场强度E=32V/m．
（2）设小球在N点速率为v2，在N点由牛顿第二定律得：qv2B=m
从M到N点，由机械能守恒定律得：
mgR+
mv12=
mv22
联立两式解得：B=5
T．
故所加磁场的磁感应强度B=5
T．
mg=m
| v12 |
| R |
在水平轨道上，对小球运用动能定理得：
qEd=
| 1 |
| 2 |
| 1 |
| 2 |
联立两式解得：E=32V/m．
故所加电场的电场强度E=32V/m．
（2）设小球在N点速率为v2，在N点由牛顿第二定律得：qv2B=m
| v22 |
| R |
从M到N点，由机械能守恒定律得：
mgR+
| 1 |
| 2 |
| 1 |
| 2 |
联立两式解得：B=5
| 3 |
故所加磁场的磁感应强度B=5
| 3 |
练习册系列答案
相关题目
（2010?南通模拟）某塑料球成型机工作时，可以喷出速度v0=10m/s的塑料小球，已知喷出小球的质量m=1.0×10-4 kg，并且在喷出时已带了q=1.0×10-4 C的负电荷，如图所示，小球从喷口飞出后，先滑过长d=1.5m的水平光滑的绝缘轨道，而后又过半径R=0.4m的圆弧形竖立的光滑绝缘轨道．今在水平轨道上加上水平向右的电场强度为E的匀强电场，小球将恰好从圆弧轨道的最高点M处水平飞出；若再在圆形轨道区域加上垂直于纸面向里的匀强磁场后，小球将恰好从圆形轨道上与圆心等高的N点脱离轨道落入放在地面上接地良好的金属容器内，g=10m/s2，求：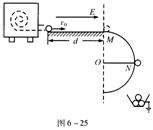
某塑料球成型机工作时，可以喷出速度v0 = 10 m/s的塑料小球，已知喷出的每个小球的质量m = 1.0 × 10 – 4 kg，并且在喷出时已带了q = – 1.0 × 10 – 4 C的电荷量．如图6 – 25所示，小球从喷口飞出后，先滑过长d = 1.5 m的水平光滑的绝缘轨道，而后又滑过半径R = 0.4 m的圆弧形竖立的光滑绝缘轨道并从某处飞出．今在水平轨道上加上水平向右的场强大小为E的匀强电场，小球将恰好从圆弧轨道的最高点M处水平飞出；若再在圆形轨道区域加上垂直纸面向里的匀强磁场后，小球将恰好滑过圆弧轨道上与圆心等高的N点，最后落入放在地面上接地良好的金属容器内，g = 10 m/s2，求
