题目内容
12. 如图,m1=2kg,m2=4kg,两者间用一劲度系数为100N/m的轻弹簧相连,两物体与倾角为37°的斜面间的动摩擦因数都为μ=0.25.现用沿斜面方向的力F拉着两物体匀速向上运动.求F应为多大?弹簧伸长了多少?(取g=10m/s2)
如图,m1=2kg,m2=4kg,两者间用一劲度系数为100N/m的轻弹簧相连,两物体与倾角为37°的斜面间的动摩擦因数都为μ=0.25.现用沿斜面方向的力F拉着两物体匀速向上运动.求F应为多大?弹簧伸长了多少?(取g=10m/s2)
分析 对整体受力分析,根据共点力平衡取得拉力,然后对m1受力分析,根据共点力平衡求的弹簧的弹力,根据F=kx求的弹簧的伸长量
解答 解:对整体受力分析,有共点力平衡可得F-μ(m1+m2)gcosθ-(m1+m2)gsinθ=0
解得F=μ(m1+m2)gcosθ+(m1+m2)gsinθ=48N
对m1受力分析,根据共点力平衡可得F弹-μm1gcosθ-m1gsinθ=0
解得F弹=μm1gcosθ+m1gsinθ=16N
由F弹=kx可得
x=$\frac{{F}_{弹}}{k}=\frac{16}{100}m=0.16m$
答:F应为48N,弹簧伸长了0.16m
点评 本题主要考查了共点力下的平衡,关键是合理的利用整体法和隔离法对物体受力分析

练习册系列答案
相关题目
20.2013年6月13日,北京时间6月13日13时18分,天宫一号目标飞行器与神十飞船在离地面343Km的近圆轨道上进行了我国第5次载入空间交会对接.神舟十号航天员成功开启天宫一号目标飞行器舱门,聂海胜、张晓光、王亚平以漂浮姿态进入天宫一号.下列说法正确的是( )
| A. | 航天员以漂浮姿态进入天宫一号,说明航天员不受地球引力作用 | |
| B. | 完成对接后组合体的运行速度小于7.9Km/s | |
| C. | 王亚平在天宫一号中讲课时可以用弹簧秤悬挂测一杯水的重力 | |
| D. | 完成对接后的组合体运行的加速度一定小于9.8m/s2 |
7. 在绝缘水平面上,两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交P、Q连线于O点,A为MN上的一点.一带负电荷的小球,从A点由静止释放,只在静电力作用下运动,取无限远处的电势为零,则( )
在绝缘水平面上,两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交P、Q连线于O点,A为MN上的一点.一带负电荷的小球,从A点由静止释放,只在静电力作用下运动,取无限远处的电势为零,则( )
 在绝缘水平面上,两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交P、Q连线于O点,A为MN上的一点.一带负电荷的小球,从A点由静止释放,只在静电力作用下运动,取无限远处的电势为零,则( )
在绝缘水平面上,两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交P、Q连线于O点,A为MN上的一点.一带负电荷的小球,从A点由静止释放,只在静电力作用下运动,取无限远处的电势为零,则( )| A. | 小球由A向O的运动过程中加速度可能先增大后减小 | |
| B. | 小球会在MN连线上以O为对称点运动 | |
| C. | PQ连线中O点的电势最高 | |
| D. | 若在A点把小球以一定初速度抛出,小球有可能做圆周运动 |
2.一物体从某高度自由落下,空气阻力忽略不计,经6s落地,则物体落地前1s内的位移为(g=10m/s2)( )
| A. | 5m | B. | 180m | C. | 55m | D. | 125m |
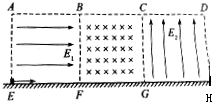 如图所示,在绝缘水平桌面上方有一竖直方向的矩形区域,该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的,且矩形的下边EH与桌面相接,三个正方形区域中分别存在方向为水平向右的匀强电场E1,垂直纸面向里的磁感应强度为B的磁场,竖直向上的匀强电场E2.其中qE2=2mg,B=$\frac{m}{q}$$\sqrt{\frac{2g}{L}}$,现有一带正电的滑块从E点开始向右做初速为零的直线运动,滑块经F、G点最终恰从D点射出电场区,桌面与滑块之间的动摩擦因素μ=0.5,重力加速度为g,滑块可视为质点,滑块质量为m,带电量为q,求:
如图所示,在绝缘水平桌面上方有一竖直方向的矩形区域,该区域是由三个边长均为L的正方形区域ABFE、BCGF和CDHG首尾相接组成的,且矩形的下边EH与桌面相接,三个正方形区域中分别存在方向为水平向右的匀强电场E1,垂直纸面向里的磁感应强度为B的磁场,竖直向上的匀强电场E2.其中qE2=2mg,B=$\frac{m}{q}$$\sqrt{\frac{2g}{L}}$,现有一带正电的滑块从E点开始向右做初速为零的直线运动,滑块经F、G点最终恰从D点射出电场区,桌面与滑块之间的动摩擦因素μ=0.5,重力加速度为g,滑块可视为质点,滑块质量为m,带电量为q,求: