题目内容
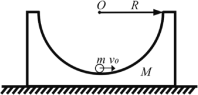
【题目】如图所示,光滑水平面上静止着质量m1=0.1kg的小球甲和质量m2 =0.2kg的小球乙,两球用轻绳连接并压紧一轻弹簧,弹簧与两小球均不拴接,初始时弹簧的压缩量x=3cn;在甲球的右侧x1处停放着质量m3=0.3kg,半径R=12cm的![]() 圆弧槽丙,槽的各个表面均光滑,下端与水平面相切。现烧断甲、乙之间的细线。且弹簧恢复原状前,甲球没有接触槽内。小球可视为质点,重力加速度g取10 m/s2。求:
圆弧槽丙,槽的各个表面均光滑,下端与水平面相切。现烧断甲、乙之间的细线。且弹簧恢复原状前,甲球没有接触槽内。小球可视为质点,重力加速度g取10 m/s2。求:
(1)x1至少为多少;
(2)若甲球恰好能到达圆弧槽丙的顶端A,初始时弹簧储存的弹性势能EP为多少;
(3)若初始时弹簧储存的弹性势能EP =1.20J,则甲球与圆弧槽丙作用后再次到达水平面时的速度为多少。

【答案】(1)2cm;(2)0.24J;(3)![]()
【解析】
(1)设弹簧恢复原状的瞬间,甲球恰好没有接触圆弧槽丙,甲的速度大小为v1、位移为x1,乙的速度大小为v2、位移为x2,由动量守恒定律
0=m1v1-m2v2
则有
0=m1x1-m2x2
由于
x1+x2=x
解得
x1=2cm
(2)弹簧恢复原状时,甲的速度大小设为v1,乙的速度大小设为v2,由动量守恒和能量守恒得
0=m1v1-m2v2
![]()
解得
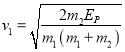 ①
①
甲与丙作用,到达顶端A时,获得的共同速度设为v3,由动量守恒和能量守恒得
![]()
![]()
![]() ②
②
由①②式得
![]()
(3)由第(2)问知,若EP=1.20J,甲球会从圆弧槽丙的A端飞出做斜抛运动,由于甲斜抛时与丙的水平速度相等,所以甲球下落时,还会再与丙作用一次,当甲落回水平面时,相当于甲、丙发生了一次弹性碰撞。
由①式知弹簧恢复原状时,甲球获得的速度v1=4.0m/s甲与丙发生弹性碰撞,设碰后甲的速度为![]() 、丙的速度为
、丙的速度为![]() ,由动量守恒和动能守恒得
,由动量守恒和动能守恒得
![]()
![]()
解得
![]()

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目