题目内容
某同学用实验的方法探究影响单摆周期的因素.
①他组装单摆时,在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,如图1所示.这样做的目的是 (填字母代号).
A.保证摆动过程中摆长不变B.可使周期测量得更加准确
C.需要改变摆长时便于调节D.保证摆球在同一竖直平面内摆动
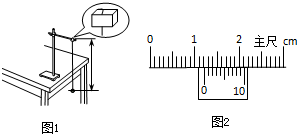
②他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图2所示,则该摆球的直径为 mm,单摆摆长为 m.
③如图振动图象真实地描述了对摆长为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是 (填字母代号).

①他组装单摆时,在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,如图1所示.这样做的目的是

A.保证摆动过程中摆长不变B.可使周期测量得更加准确
C.需要改变摆长时便于调节D.保证摆球在同一竖直平面内摆动
②他组装好单摆后在摆球自然悬垂的情况下,用毫米刻度尺从悬点量到摆球的最低端的长度L=0.9990m,再用游标卡尺测量摆球直径,结果如图2所示,则该摆球的直径为
③如图振动图象真实地描述了对摆长为1m的单摆进行周期测量的四种操作过程,图中横坐标原点表示计时开始,A、B、C均为30次全振动的图象,已知sin5°=0.087,sin15°=0.26,这四种操作过程合乎实验要求且误差最小的是

分析:当摆角小于等于5°时,我们认为小球做单摆运动,游标卡尺的示数等于主尺示数与游标尺示数之和;摆长为悬点到球心的距离;对于测量误差可根据实验原理进行分析;
解答:解:(1)在摆线上端的悬点处,用一块开有狭缝的橡皮夹牢摆线,再用铁架台的铁夹将橡皮夹紧,是为了防止动过程中摆长发生变化,如果需要改变摆长来探究摆长与周期关系时,方便调节摆长,故AC正确,
故选AC
(2)游标卡尺示数为:d=12mm+1×0.1mm=12.1mm;
单摆摆长为L=l-
=0.9990m-0.00605m=0.99295m
(3)当摆角小于等于5°时,我们认为小球做单摆运动,所以振幅约为:1×0.087m=8.7cm,当小球摆到最低点开始计时,误差较小,测量周期时要让小球做30-50次全振动,求平均值,所以A合乎实验要求且误差最小
故选A
故答案为:①AC ②12.1 0.99295 ③A
故选AC
(2)游标卡尺示数为:d=12mm+1×0.1mm=12.1mm;
单摆摆长为L=l-
| d |
| 2 |
(3)当摆角小于等于5°时,我们认为小球做单摆运动,所以振幅约为:1×0.087m=8.7cm,当小球摆到最低点开始计时,误差较小,测量周期时要让小球做30-50次全振动,求平均值,所以A合乎实验要求且误差最小
故选A
故答案为:①AC ②12.1 0.99295 ③A
点评:掌握单摆的周期公式,从而求解加速度,摆长、周期等物理量之间的关系.单摆的周期采用累积法测量可减小误差.对于测量误差可根据实验原理进行分析.

练习册系列答案
相关题目
近年来,因中国的“嫦娥探月”、美国的火箭撞月、印度的“月船一号”等让公众重新燃起了对月球的激情.某同学在物理学习中记录了一些与地球、月球有关的数据资料为:地球半径R=6400km,月球半径r=1740km,地球表面重力加速度g0=9.80m/s2,月球表面重力加速度g′=1.56m/s2,月球绕地球转动的线速度v=1000m/s,月球绕地球转动一周的时间T=27.3天,光速c=2.998×105km/s,假设某次实验中用激光器向位于头顶正上方的月球表面发射出的激光光束,经过约t=2.565s接收到从月球表面发射回来的激光信号,利用上述数据可算出地球表面与月球表面之间的距离s,则下列方法正确的是( )
A、利用激光束的发射,用s=cg
| ||
B、利用月球运动的线速度及周期关系v=
| ||
C、利用地球表面的重力加速度、地球半径及月球运动的 线速度关系m月g0=m月
| ||
D、利用月球表面的重力加速度、地球半径及月球运动周期关系m月g′=m月
|

