题目内容
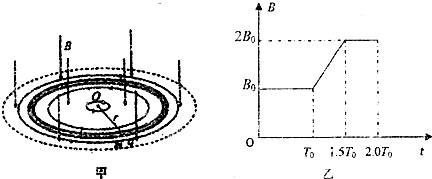
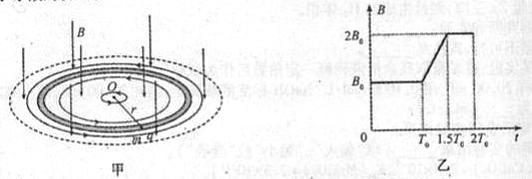
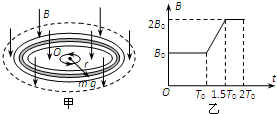 如图甲,在圆柱形区域内存在一方向竖直向下、磁感应强度大小为B的匀强磁场,在此区域内,沿水平面固定一半径为r的圆环形光滑细玻璃管,环心O在区域中心.一质量为m、带电荷量为q(q?0)的小球,在管内沿逆时针方向(从上向下看)做圆周运动.已知磁感应强度大小B随时间t的变化关系如图乙所示,其中T0=
如图甲,在圆柱形区域内存在一方向竖直向下、磁感应强度大小为B的匀强磁场,在此区域内,沿水平面固定一半径为r的圆环形光滑细玻璃管,环心O在区域中心.一质量为m、带电荷量为q(q?0)的小球,在管内沿逆时针方向(从上向下看)做圆周运动.已知磁感应强度大小B随时间t的变化关系如图乙所示,其中T0=| 2πm | qB0 |
(1)在t=0到t=T0这段时间内,小球不受细管侧壁的作用力,求小球的速度大小v0;
(2)在竖直向下的磁感应强度增大过程中,将产生涡旋电场,其电场线是在水平面内一系列沿逆时针方向的同心圆,同一条电场线上各点的场强大小相等.试求t=T0到t=1.5T0这段时间内:
①细管内涡旋电场的场强大小E;
②电场力对小球做的功W.
分析:(1)在t=0到t=T0这段时间内,小球不受细管侧壁的作用力,说明洛伦兹力提供向心力,根据牛顿第二定律列式求解;
(2)①根据法拉第电磁感应定律求解出感应电动势,再进一步计算电场强度;
②先根据牛顿第二定律求解加速度,计算出路程,再求解电场力的功.
(2)①根据法拉第电磁感应定律求解出感应电动势,再进一步计算电场强度;
②先根据牛顿第二定律求解加速度,计算出路程,再求解电场力的功.
解答:解:(1)在t=0到t=T0这段时间内,小球不受细管侧壁的作用力,说明洛伦兹力提供向心力,根据牛顿第二定律,有
qv0B0=m
解得
v0=
(2)①根据法拉第电磁感应定律,感应电动势为:U=
=πr2?
=
电势差与电场强度的关系,有:U=E?2πr
由上面两式解得
E=
=
其中:T0=
故:E=
②电场力为:F=Eq=
;
根据牛顿第二定律,有
F=ma
解得
a=
物体的末速度为:v=v0+at=
+
?
=
根据动能定理,电场力做的功为:W=
mv2-
m
=
;
答:(1)在t=0到t=T0这段时间内,小球的速度大小为
;
(2)在t=T0到t=1.5T0这段时间内:
①细管内涡旋电场的场强大小E为
;
②电场力对小球做的功W为
.
qv0B0=m
| ||
| r |
解得
v0=
| qB0r |
| m |
(2)①根据法拉第电磁感应定律,感应电动势为:U=
| S△B |
| △t |
| B0 | ||
|
| 2πr2B0 |
| T0 |
电势差与电场强度的关系,有:U=E?2πr
由上面两式解得
E=
| U |
| 2πr |
| r B0 |
| T0 |
其中:T0=
| 2πm |
| qB0 |
故:E=
qr0
| ||
| 2πm |
②电场力为:F=Eq=
| r B0q |
| T0 |
根据牛顿第二定律,有
F=ma
解得
a=
| r B0q |
| mT0 |
物体的末速度为:v=v0+at=
| qB0r |
| m |
| r B0q |
| mT0 |
| T0 |
| 2 |
| 3qB0r |
| 2m |
根据动能定理,电场力做的功为:W=
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
5q2
| ||
| 8m |
答:(1)在t=0到t=T0这段时间内,小球的速度大小为
| qB0r |
| m |
(2)在t=T0到t=1.5T0这段时间内:
①细管内涡旋电场的场强大小E为
qr0
| ||
| 2πm |
②电场力对小球做的功W为
5q2
| ||
| 8m |
点评:本题是有关感应加速器的问题,感生电场的电场力做正功,电场力是恒定大小的力,电荷速率随着时间均匀增加,结合动能定理、电势差与电场强度的关系公式、牛顿第二定律列式求解.

练习册系列答案
相关题目
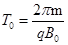 。设小球在运动过程中电量保持不变,对原磁场的影响可忽略。
。设小球在运动过程中电量保持不变,对原磁场的影响可忽略。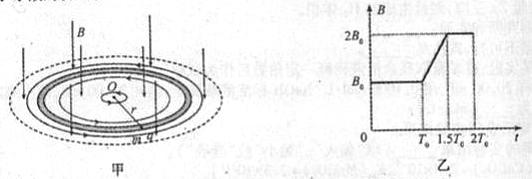
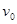 ;
;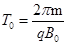 。设小球在运动过程中电量保持不变,对原磁场的影响可忽略。
。设小球在运动过程中电量保持不变,对原磁场的影响可忽略。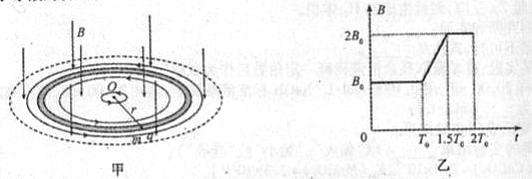
 ;
;