题目内容
3.如图所示,OAB为竖直放置的轻质等腰三角形支架,θ=30°,AB长为2L,C为AB的中点,A端搁在支撑物上,OA水平,支架可绕过O点的水平轴自由转动,质量为M=$\frac{11}{16}$m带正电的物块P固定在支架上的A点.现将另一质量为m、电荷量为+q的物块Q由中点C静止释放,Q沿斜面向上运动,刚好能到达B点,此时支架恰好不翻倒.已知Q与斜面间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{6}$,P、Q均可视为点电荷,求:
(1)C、B两点间的电势差;
(2)释放Q瞬间,它的加速度;
(3)若Q运动过程中的最大速度为v,求Q处于平衡状态时的总势能.(以C点为重力势能和电势能的零点)
分析 (1)对物块Q,根据动能定理解得C、B两点间的电势差;
(2)Q即将到达B点时,P受到的库仑力为FB,对支架,由力矩的平衡列式,求解FB,Q在C点时,根据库仑定律求解FC,再根据牛顿第二定律求解加速度;
(3)Q处于平衡状态时,有两个位置,由能量守恒定律结合库仑定律求解.
解答 解:(1)对物块Q,根据动能定理有:UCBq-mgLsinθ-mgcosθμL=0,
解得:${U_{CB}}=\frac{3mgL}{4q}$,
(2)Q即将到达B点时,P受到的库仑力为FB,对支架,由力矩的平衡有:$NL+fLtanθ=Mg\frac{L}{cosθ}+{F_B}Ltanθ$,
对Q:$N=mgcosθ=\frac{{\sqrt{3}}}{2}mg$,$f=μN=\frac{1}{4}mg$,
解得:${F_B}=\frac{3}{8}mg$,
Q在C点时,受到的库仑力为FC,则:$\frac{{F}_{C}}{{F}_{B}}=\frac{\frac{kQq}{{L}^{2}}}{\frac{kQq}{(2L)^{2}}}=4$,
解得:${F_C}=\frac{3}{2}mg$
释放Q瞬间:FC-mgsinθ-f=ma
解得:$a=\frac{3}{4}g$
(3)Q处于平衡状态时,有两个位置.
Q经过最大速度为v的位置,Q受到的库仑力为F,则:$F=mgsinθ+f=\frac{3}{4}mg$
又:$\frac{{F}_{\;}}{{F}_{C}}=\frac{\frac{kQq}{{{L}_{1}}^{2}}}{\frac{kQq}{{L}^{2}}}=\frac{{L}^{2}}{{{L}_{1}}^{2}}$
解得:${L_1}=\sqrt{2}L$
此位置,Q的总势能为EP1,由能量守恒定律有:$0=\frac{1}{2}m{v^2}+{E_{P1}}+f({L_1}-L)$
解得:${E_{P1}}=-\frac{{\sqrt{2}-1}}{4}mgL-\frac{1}{2}m{v^2}$
Q到达B点后,因$mgsinθ-{F_B}=\frac{1}{8}mg$<f,故Q停在B点,Q的总势能为EP2,
则:${E_{P2}}=mgLsinθ-{U_{CB}}q=\frac{1}{2}mgL-\frac{3}{4}mgL=-\frac{1}{4}mgL$
故Q处于平衡状态时的总势能为:${E_{P1}}=-\frac{{\sqrt{2}-1}}{4}mgL-\frac{1}{2}m{v^2}$或${E_{P2}}=-\frac{1}{4}mgL$
答:(1)C、B两点间的电势差为$\frac{3mgL}{4q}$;
(2)释放Q瞬间,它的加速度为$\frac{3}{4}g$;
(3)若Q运动过程中的最大速度为v,则Q处于平衡状态时的总势能为$-\frac{\sqrt{2}-1}{4}mgL-\frac{1}{2}m{v}^{2}$或$-\frac{1}{4}mgL$.
点评 本题主要考查了动能定理、牛顿第二定律、库仑定律以及能量守恒定律的直接应用,要求同学们正确正确分析物块的受力情况和运动情况,注意Q处于平衡状态时,有两个位置,难度适中.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案| A. | 有弹力必有摩擦力 | |
| B. | 有摩擦力必有弹力 | |
| C. | 摩擦力的大小正比于弹力的大小 | |
| D. | 弹力方向与摩擦力方向一定互相垂直 |
| A. | 大小为a1-a2 | B. | 大小为$\sqrt{{{a}_{1}}^{2}+{{a}_{2}}^{2}}$ | ||
| C. | 方向为东偏北arctan $\frac{a_2}{a_1}$ | D. | 方向为与较大的力同向 |
 如图所示,水平放置的两个平行金属板,上板带负电,下板带等量的正电,三个质量相等,分别带正电、负电和不带电的粒子从极板的左侧P点以相同的水平初速度进入电场中,分别落在正极板的a、b、c三处,由此可知( )
如图所示,水平放置的两个平行金属板,上板带负电,下板带等量的正电,三个质量相等,分别带正电、负电和不带电的粒子从极板的左侧P点以相同的水平初速度进入电场中,分别落在正极板的a、b、c三处,由此可知( )| A. | 粒子a带正电,b不带电,c带负电 | |
| B. | 三个粒子在电场中运动的时间相等 | |
| C. | 三个粒子在电场中的加速度aa<ab<ac | |
| D. | 三个粒子到达正极板的动能Eka>Ekb>Ekc |
 如图,若两颗人造卫星a和b均绕地球做匀速圆周运单,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )
如图,若两颗人造卫星a和b均绕地球做匀速圆周运单,且a、b在运动过程中仅受地球万有引力的作用,a、b绕地球运动的线速度大小分别为v1、v2,周期分别为T1、T2,则( )| A. | $\frac{{v}_{1}}{{v}_{2}}=(\frac{{T}_{2}}{{T}_{1}})^{\frac{1}{3}}$ | B. | $\frac{{v}_{1}}{{v}_{2}}$=$\frac{{T}_{2}}{{T}_{1}}$ | ||
| C. | $\frac{{v}_{1}}{{v}_{2}}$=($\frac{{T}_{1}}{{T}_{2}}$)${\;}^{\frac{1}{3}}$ | D. | $\frac{{v}_{1}}{{v}_{2}}$=($\frac{{T}_{2}}{{T}_{1}}$)3 |
| A. | 库仑在探究点电荷问相互作用力大小时,采用了控制变量法 | |
| B. | 库仑在探究点电荷问相互作用力大小时,采用了等效替代法 | |
| C. | 在探究平行板电容器的电容与哪些因素有关时,采用了控制变量法 | |
| D. | 在探究平行板电容器的电容与哪些因素有关时,采用了理想模型法 | |
| E. | 用比值法定义的物理概念在物理学中占有相当大的比例,例如场强E=$\frac{F}{q}$,电容C=$\frac{Q}{U}$,电阻R=$\frac{U}{I}$都是采用比值法定义的 |
 小明家中有一个具有保温功能的电饭锅,从它的说明书上收集到如表中的数据,电饭锅的电路原理图如图所示.请问:
小明家中有一个具有保温功能的电饭锅,从它的说明书上收集到如表中的数据,电饭锅的电路原理图如图所示.请问:| 额定电压 | 220V |
| 频率 | 50Hz |
| 加热功率 | 880W |
| 保温功率 | 40W |
| 最大容积 | 3L |
(2)该电饭锅正常加热30分钟后保温1小时共用电多少KWh?

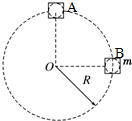 如图所示,质量为m的小球置于正方体的光滑硬质盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使盒子在最高点A时盒子与小球之间恰好无作用力,则该盒子在B点(与圆心O等高)时的速度大小为$\sqrt{gR}$、盒子对球的作用力大小为$\sqrt{2gR}$.
如图所示,质量为m的小球置于正方体的光滑硬质盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计,要使盒子在最高点A时盒子与小球之间恰好无作用力,则该盒子在B点(与圆心O等高)时的速度大小为$\sqrt{gR}$、盒子对球的作用力大小为$\sqrt{2gR}$.