题目内容
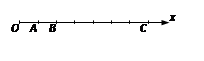
弹簧振子以O点为平衡位置，在B、C两点间做简谐运动.在t＝0时刻，振子从O、B间的P 点以速度v向B点运动；在t="0.20" s时，振子速度第一次变为-v；在t="0.50" s时，振子速度第二次变为-v.
(1)求弹簧振子振动的周期T；
(2)若B、C之间的距离为25 cm，求振子在4.0 s内通过的路程.
(1)求弹簧振子振动的周期T；
(2)若B、C之间的距离为25 cm，求振子在4.0 s内通过的路程.
：(1) 1.00 s(2) 200 cm
解：(1)由对称性tPB＝tBP＝0.10 s……1′
同理，tPO＝tOP′=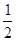
×0.30 s=0.15s……1′
故tBO=tBP+tPO=T/4……1′
所以 T＝4×(0.10+0.15) s＝1.00 s.
即周期为1.00 s.……1′
(2)
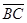="2A=25" cm，振幅A＝12.5 cm……2′
因振子1个周期通过4A的路程，
故在4.0 s＝4T内通过s＝4×4A＝200 cm.……2′
本题考查简谐运动，简谐运动具有对称性，在做题特别关于时间时，一定要注意，根据对称性可tPB＝tBP＝0.10 s tPO＝tOP′=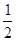×0.30 s=0.15s从而算出tBO=tBP+tPO=T/4得出周期，因振子1个周期通过4A的路程，可算在4s内的路程
同理，tPO＝tOP′=
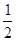×0.30 s=0.15s……1′故tBO=tBP+tPO=T/4……1′
所以 T＝4×(0.10+0.15) s＝1.00 s.
即周期为1.00 s.……1′
(2)
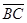="2A=25" cm，振幅A＝12.5 cm……2′因振子1个周期通过4A的路程，
故在4.0 s＝4T内通过s＝4×4A＝200 cm.……2′
本题考查简谐运动，简谐运动具有对称性，在做题特别关于时间时，一定要注意，根据对称性可tPB＝tBP＝0.10 s tPO＝tOP′=
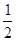×0.30 s=0.15s从而算出tBO=tBP+tPO=T/4得出周期，因振子1个周期通过4A的路程，可算在4s内的路程
练习册系列答案
冲刺100分1号卷系列答案
相关题目
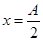处所经最短时间为
，第一次从最大正位移处运动到
，关于
，
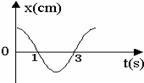
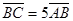，质点O在垂直于x轴方向做简谐运动，沿x轴传播形成横波．t = 0时刻，O点开始向上运动，经t = 0.2s，O点第一次到达上方最大位移处，这时A点刚好开始运动．那么在t = 2.5s时刻，关于质点B和C运动情况, 以下描述中正确的是
