题目内容
一个做简谐运动的弹簧振子,周期为T,振幅为A,设振子第一次从平衡位置运动到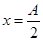 处所经最短时间为
处所经最短时间为 ,第一次从最大正位移处运动到
,第一次从最大正位移处运动到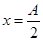 所经最短时间为
所经最短时间为 ,关于
,关于 与
与 ,下列说法正确的是( )
,下列说法正确的是( )
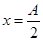 处所经最短时间为
处所经最短时间为 ,第一次从最大正位移处运动到
,第一次从最大正位移处运动到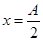 所经最短时间为
所经最短时间为 ,关于
,关于 与
与 ,下列说法正确的是( )
,下列说法正确的是( )| A.t1=t2 | B.t1<t2 | C.t1>t2 | D.无法判断 |
B
【错解分析】错解一:因为周期为T,那么,从平衡位置到
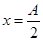 处正好是振幅的一半,所以时间为
处正好是振幅的一半,所以时间为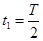 ,同理
,同理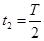 ,所以选A。
,所以选A。错解二:振子从平衡位置向
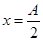 处移动,因为回复力小,所以加速度也小,从而最大位移处(即
处移动,因为回复力小,所以加速度也小,从而最大位移处(即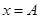 )向
)向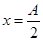 处移动,回复力大,加速度也大,因而时间短,所以t1>t2,应选C。
处移动,回复力大,加速度也大,因而时间短,所以t1>t2,应选C。错解三:因为这是一个变加速运动问题,不能用匀速运动或匀变速运动规律求解,因而无法判断t1和t2的大小关系,所以选D。
主要是对简谐运动的特殊运动规律不清楚,只记住了周期公式,没注意分析简谐运动的全过程,没能深入地理解和掌握这种运动形式的特点。因而解题时错误地沿用了匀速或匀变速运动的规律,选择A的同学就是用匀速运动规律去解,而选择C的同学用了匀变速运动规律去解,因而错了。事实上,简谐运动的过程有其自身的许多规律,我们应该用它的特殊规律去求解问题,而不能用匀速或匀变速运动规律去求解。
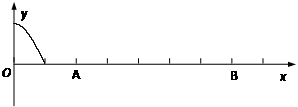
【正解】方法一:用图象法,画出x-t图象,从图象上,我们可以很直观地看出:t1<t2,因而正确答案为:B。
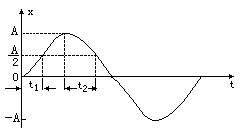
方法二:从图象为正弦曲线和数学知识可写出位移随时间的函数关系式,物理学上称为振动方程,从平衡位置开始,振子的振动方程为:
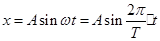 ,当
,当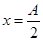 ,最短时间
,最短时间 ,即
,即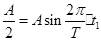
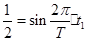
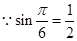
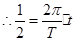
解得:
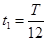
而振子从最大位移处到
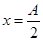 处最短时间为
处最短时间为 ,即
,即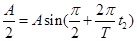
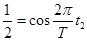
解得:
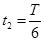 。可以得出结论
。可以得出结论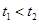 ,选B
,选B【点评】以上两种方法,第一种方法是定性分析,在选择题练习时,是要重点掌握的。第二种方法可以进行定量计算,但由于要涉及振动方程,所以不做统一要求。
另外,由于震动具有周期性,从平衡位置计时,振子到达
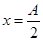 处的时间可以表达为
处的时间可以表达为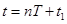 ,从最大位移处到达
,从最大位移处到达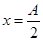 处的时间可以表达为t'=" nT" + t2。此处,为了题目简明起见,题文中用了“第一次”和“最短时间”等字样。否则就无法比较两个过程所用时间的长短。
处的时间可以表达为t'=" nT" + t2。此处,为了题目简明起见,题文中用了“第一次”和“最短时间”等字样。否则就无法比较两个过程所用时间的长短。
练习册系列答案
相关题目


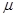 ,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)
,要使砝码与滑块在振动过程中不发生相对运动,问最大振幅等于多少?(设最大静摩擦力等于滑动摩擦力)