题目内容
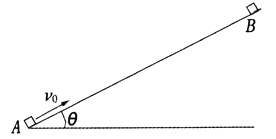
【题目】如图,倾角![]() =37°的固定斜面长L=2.1m,t=0时刻小滑块A从斜面底端以速度v0=5m/s沿斜面向上运动,同时小滑块B从斜面顶端由静止开始沿斜面下滑。它们与斜面间的动摩擦因数均为
=37°的固定斜面长L=2.1m,t=0时刻小滑块A从斜面底端以速度v0=5m/s沿斜面向上运动,同时小滑块B从斜面顶端由静止开始沿斜面下滑。它们与斜面间的动摩擦因数均为![]() =0.5。两滑块质量均为m,且均可视为质点。取g=10m/s2,sin37°=0.6,cos37°=0.8。则
=0.5。两滑块质量均为m,且均可视为质点。取g=10m/s2,sin37°=0.6,cos37°=0.8。则
(1)两滑块何时相遇?
(2)相遇时A滑块距斜面底端多远?
【答案】(1) ![]() (2)
(2) ![]()
【解析】 (1)滑块沿斜面向上或向下运动时,由牛顿第二定律:
![]()
![]()
解得a1=10m/s2 a2=2m/s2
设滑块A沿斜面上滑的最远距离为想,根据运动公式:0-v02=-2a1x1
解得x1=1.25m
滑块沿斜面向上运动的时间:![]()
此过程中滑块B沿斜面下滑的距离:![]()
解得x2=0.25m
此时两滑块相距:L=L-x1-x2
解得L=0.6m
此时滑块的速度:v2=a2t1=1m/s
之后滑块AB均沿斜面向下运动,设再经过t2时间它们相遇,则![]()
![]()
![]()
解得t2=0.6s
即经t=t1+t2=1.1s时刻,两滑块相遇.
(2)相遇时,滑块B下滑的距离![]()
此时滑块A距离斜面底端x=L-xB
解得x=0.89m

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目