题目内容
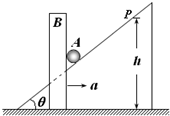 (2009?普陀区二模)如图所示,薄板形斜面体竖直固定在水平地面上,其倾角为θ=37°.一个“Π”的物体B靠在斜面体的前后两侧,并可在水平面上自由滑动而不会倾斜,B的质量为M=2kg.一根质量为m=1kg的光滑细圆柱体A搁在B的竖直面和斜面之间.现推动B以水平加速度a=4m/s2向右运动,并带动A沿斜面方向斜向上运动.所有摩擦都不计,且不考虑圆柱体的滚动,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(2009?普陀区二模)如图所示,薄板形斜面体竖直固定在水平地面上,其倾角为θ=37°.一个“Π”的物体B靠在斜面体的前后两侧,并可在水平面上自由滑动而不会倾斜,B的质量为M=2kg.一根质量为m=1kg的光滑细圆柱体A搁在B的竖直面和斜面之间.现推动B以水平加速度a=4m/s2向右运动,并带动A沿斜面方向斜向上运动.所有摩擦都不计,且不考虑圆柱体的滚动,g=10m/s2,sin37°=0.6,cos37°=0.8.求:(1)圆柱体A的加速度大小;
(2)B物体对A的推力F的大小;
(3)当A被缓慢推至离地高为h=1m的P处时停止运动,放手后A下滑时带动B一起运动,当到达斜面底端时B的速度为多大?
分析:(1)A的合加速度方向沿斜面向上,其水平向右的分加速度和B的加速度相同,根据几何关系即可求解;
(2)对A运用牛顿第二定律即可求解;
(3)由机械能守解恒定律及A和B的速度关系即可求解.
(2)对A运用牛顿第二定律即可求解;
(3)由机械能守解恒定律及A和B的速度关系即可求解.
解答:解:(1)A的合加速度方向沿斜面向上,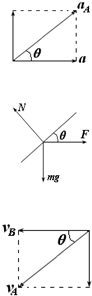
其水平向右的分加速度和B的加速度相同,
则aA=
代入数据解得 aA=5m/s2
(2)对A,由牛顿第二定律 Fcos37°-mgsin37°=maA
代入数据解得 F=13.75N
(3)mgh=
m
+
M
又 vB=vAcos37°
联立解得 vB=
m/s (或2.4m/s)
答:(1)圆柱体A的加速度大小为5m/s2;
(2)B物体对A的推力F的大小为13.75N;
(3)到达斜面底端时B的速度为
m/s (或2.4m/s).

其水平向右的分加速度和B的加速度相同,
则aA=
| a |
| cos370 |
代入数据解得 aA=5m/s2
(2)对A,由牛顿第二定律 Fcos37°-mgsin37°=maA
代入数据解得 F=13.75N
(3)mgh=
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 B |
又 vB=vAcos37°
联立解得 vB=
|
答:(1)圆柱体A的加速度大小为5m/s2;
(2)B物体对A的推力F的大小为13.75N;
(3)到达斜面底端时B的速度为
|
点评:本题要注意A和B的加速度之间的关系,再结合牛顿第二定律和机械能守恒定律去解题,难度适中.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
 (2009?普陀区二模)两个相同的可视为质点的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两个小球,然后,用一水平方向的力F作用在小球A上,此时三根线均处于伸直状态,且OB细线恰好处于竖直方向如图所示.如果两小球均处于静止状态,则力F的大小为( )
(2009?普陀区二模)两个相同的可视为质点的小球A和B,质量均为m,用长度相同的两根细线把A、B两球悬挂在水平天花板上的同一点O,并用长度相同的细线连接A、B两个小球,然后,用一水平方向的力F作用在小球A上,此时三根线均处于伸直状态,且OB细线恰好处于竖直方向如图所示.如果两小球均处于静止状态,则力F的大小为( ) (2009?普陀区二模)如图所示,在矩形ABCD的AD边和BC边的中点M和N各放一个点电荷,它们分别带等量的正、负电荷.E、F是AB边和CD边的中点,P、Q两点在MN的连线上,MP=QN.对于E、F、P、Q四点,其中电场强度相同、电势相等的两点是( )
(2009?普陀区二模)如图所示,在矩形ABCD的AD边和BC边的中点M和N各放一个点电荷,它们分别带等量的正、负电荷.E、F是AB边和CD边的中点,P、Q两点在MN的连线上,MP=QN.对于E、F、P、Q四点,其中电场强度相同、电势相等的两点是( ) (2009?普陀区二模)如图所示,在O点处放置一个正电荷.在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(如图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法中正确的是( )
(2009?普陀区二模)如图所示,在O点处放置一个正电荷.在过O点的竖直平面内的A点,自由释放一个带正电的小球,小球的质量为m、电荷量为q.小球落下的轨迹如图中虚线所示,它与以O为圆心、R为半径的圆(如图中实线表示)相交于B、C两点,O、C在同一水平线上,∠BOC=30°,A距离OC的竖直高度为h.若小球通过B点的速度为v,则下列说法中正确的是( ) (2009?普陀区二模)如图所示,在光滑的水平面上,一质量为m,半径为r,电阻为R的均匀金属环,以v0的初速度向一磁感应强度为B的有界匀强磁场滑去(磁场宽度d>2r).圆环的一半进入磁场历时t秒,这时圆环上产生的焦耳热为Q,则t秒末圆环中感应电流的瞬时功率为( )
(2009?普陀区二模)如图所示,在光滑的水平面上,一质量为m,半径为r,电阻为R的均匀金属环,以v0的初速度向一磁感应强度为B的有界匀强磁场滑去(磁场宽度d>2r).圆环的一半进入磁场历时t秒,这时圆环上产生的焦耳热为Q,则t秒末圆环中感应电流的瞬时功率为( )