题目内容
在建筑工地上,我们常常看到工人用重锤将柱桩打入地下的情景.对此,我们可以建立这样一个力学模型:重锤的质量为m,从距桩顶高H处自由下落,柱桩的质量为M,重锤打击柱桩后不反弹且打击时间极短.柱桩受到地面的阻力恒为f,空气阻力忽略不计.利用这一模型,计算重锤一次打击柱桩时桩进入地下的深度h.一位同学这样解:设柱桩进入地面的深度为h,对全程运用动能定理,得:mf(H+h)+Mgh-fh=0可解得:h=…你认为该同学的解法是否正确?如果正确,请求出结果;如果不正确,请说明理由,并列式求出正确的结果.
分析:该同学忽略了重锤打击柱桩后不反弹的过程有能量损失,所以解法不对;
正确解法应该是先由动量守恒求得它们的公共速度,再以整体为研究对象应用动能定理求出柱桩的位移.
正确解法应该是先由动量守恒求得它们的公共速度,再以整体为研究对象应用动能定理求出柱桩的位移.
解答:解:该同学解题思路不正确;因为在重锤与柱桩碰撞过程中系统机械能有损失.
(或碰撞过程中重锤与柱桩之间的弹力做的总功不为零)
正确解答如下:
设重锤打击柱桩时的速度为v0,根据机械能守恒定律,
有mgH=
mV02 得V0=
重锤打击柱桩后不反弹成为整体设速度为v,根据动量守恒得;
mV0=(M+m)v
v=
V0
再以后重锤与柱桩一起向下运动至静止,设进入地面深度为h,根据动能定理有:
(m+M)gh-fh=0-
(m+M)v2
联立求解得h=
答;该同学忽略了撞击过程中的能量损失,故不正确;
正确求解后柱桩进入的深度h=
(或碰撞过程中重锤与柱桩之间的弹力做的总功不为零)
正确解答如下:
设重锤打击柱桩时的速度为v0,根据机械能守恒定律,
有mgH=
| 1 |
| 2 |
| 2gH |
重锤打击柱桩后不反弹成为整体设速度为v,根据动量守恒得;
mV0=(M+m)v
v=
| m |
| m+M |
再以后重锤与柱桩一起向下运动至静止,设进入地面深度为h,根据动能定理有:
(m+M)gh-fh=0-
| 1 |
| 2 |
联立求解得h=
| m3gH |
| (m+M)f-(m+M)2g |
答;该同学忽略了撞击过程中的能量损失,故不正确;
正确求解后柱桩进入的深度h=
| m3gH |
| (m+M)f-(m+M)2g |
点评:本题的关键是知道碰撞过程中有能量损失,必须由动量守恒求的撞击完后的共同速度,再由动能定理求的结论.

练习册系列答案
相关题目
 ;得出
;得出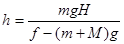 。
。