题目内容
【题目】某同学用如图的装置做“验证动量守恒定律”的实验，操作步骤如下：
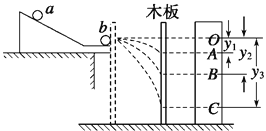
（1）先将斜槽轨道的末端调整水平，在一块平木板表面先后钉上白纸和复写纸，并将该木板竖立于靠近槽口处，使小球a从斜槽轨道上某固定点处由静止开始滚下，撞到木板在记录纸上留下压痕O。
（2）将木板向右平移适当距离，再使小球a从原固定点由静止释放，撞到木板在记录纸上留下压痕B。
（3）把半径相同的小球b静止放在斜槽轨道水平段的右边缘，让小球a仍从原固定点由静止开始滚下，与b球相碰后，两球撞在木板上，并在记录纸上留下压痕A和C。
①本实验中小球a、b的质量ma、mb关系是____________。
②放上被碰小球，两球相碰后，小球a在图中的压痕点为___________。
③记录纸上O点到A、B、C的距离y1、y2、y3，若两球碰撞动量守恒，则应满足的表达式为_________。
【答案】ma> mb C 
【解析】
（3）①本实验中要求小球a、b的质量ma、mb关系为：ma> mb，是为了避免小球a、b碰撞后小球a反弹；
②放上被碰小球b，两球相碰后，小球a平抛运动的速度减小，运动时间变长，根据y
gt2知，竖直下降的高度增大，所以在图中的压痕点为C；
③设a单独滚下经过斜槽轨道末端的速度为va，两球碰撞后a、b的速度分别为va′和vb′，若两球碰撞动量守恒，则mava＝mava′+mbvb′；根据平抛运动规律得：va
x
，va′＝x
；vb′＝x
；联立得：应满足的表达式为：
．
练习册系列答案
相关题目
