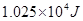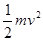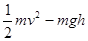题目内容
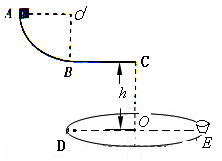
如图所示,一半径r=1m的圆盘水平放置,在其边缘 E点固定一小桶(可视为质点)。在圆盘直径 DE 的正上方平行放置一水平滑道BC ,滑道右端 C点 与圆盘圆心O在同一竖直线上,且竖直高度h =" 1.25" m。AB为一竖直面内的光滑四分之一圆弧轨道,半径R=0.45m,且与水平滑道相切与B点。一质量m=0.2kg的滑块(可视为质点)从A点由静止释放,当滑块经过C点时,圆盘从图示位置以一定的角速度ω绕通过圆心的竖直轴匀速转动,最终物块由C 点水平抛出,恰好落入圆盘边缘的小桶内.已知滑块与滑道 BC间的摩擦因数μ=0.2。(取g=10m/s2)求:
(1)滑块到达B点时受到的支持力NB的大小;
(2)水平滑道 BC的长度L;
(3)圆盘转动的角速度ω应满足的条件。

(1)滑块到达B点时受到的支持力NB的大小;
(2)水平滑道 BC的长度L;
(3)圆盘转动的角速度ω应满足的条件。
(1)6N (2)1.25m (3) 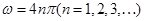
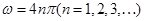
试题分析:(1)沿光滑的四分之一圆弧从A点滑到B点的过程中,只有重力做功,根据动能定理
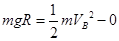 ,解得
,解得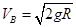 ,B点为圆周运动最低点,径向合力提供向心力有
,B点为圆周运动最低点,径向合力提供向心力有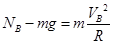 ,带入计算
,带入计算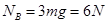 。
。(2)从C点离开水平轨道后做平抛运动,竖直方向自由落体运动高度
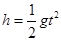 ,水平方向匀速直线运动
,水平方向匀速直线运动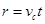 ,带入计算得
,带入计算得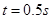 ,
,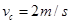 ,物体从B点滑到C点的过程中,有动能定理得
,物体从B点滑到C点的过程中,有动能定理得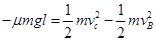 计算得
计算得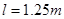
(3)当滑块经过C点时,小圆桶刚好在平抛轨迹上,要使物块恰好落在圆桶内,那么平抛的时间刚好是整数倍个周期,也就是
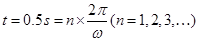 ,那么
,那么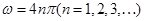

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
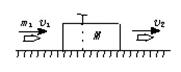
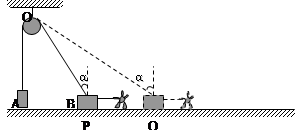
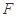 使B以
使B以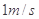 匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度
匀速的由P运动到Q,P、Q处绳与竖直方向的夹角分别为α1=37°,α2=53°.滑轮离光滑水平面高度 =2.4m,已知
=2.4m,已知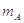 =10
=10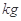 ,
,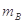 =20
=20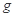 取
取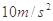 )
)