题目内容
11.一个小球以初速度v0=20m/s从某一平台上做竖直上抛运动,其重力加速度大小g=10m/s2,求:(1)小球离开平台上升的最大高度h为多少?用多少时间?
(2)第2秒内上升的高度为多少?此一秒内的平均速度为多少?前两秒内的平均速度为多少?
(3)前三秒内走的位移为多少?
(4)前四秒内走的位移为多少?
(5)前五秒内走的位移为多少?
分析 竖直上抛上升过程做匀减速直线运动,下降过程做自由落体运动,上升过程和下降过程具有对称性,结合速度位移公式求出上升的最大高度,结合速度时间公式求出上升的时间.
采用逆向思维,结合位移时间公式求出第2s内的位移,根据平均速度的定义式求出平均速度的大小.
根据位移时间公式求出物体的位移.
解答 解:(1)小球离开平台上升的最大高度为:
h=$\frac{{{v}_{0}}^{2}}{2g}=\frac{400}{20}m=20m$,
上升的时间为:t=$\frac{{v}_{0}}{g}=\frac{20}{10}s=2s$.
(2)采用逆向思维,第2s内上升的高度为:
$h′=\frac{1}{2}g{{t}_{1}}^{2}=\frac{1}{2}×10×1m=5m$,
这1s内的平均速度为:$\overline{{v}_{1}}=\frac{h′}{{t}_{1}}=\frac{5}{1}m/s=5m/s$,
前2s内的平均速度为:$\overline{v}=\frac{h}{t}=\frac{20}{2}m/s=10m/s$.
(3)规定向上为正方向,根据位移时间公式得,前3s内的位移为:
${x}_{3}={v}_{0}{t}_{3}+\frac{1}{2}a{{t}_{3}}^{2}$=$20×3-\frac{1}{2}×10×9m$=15m.
(4)根据平抛运动的对称性,知前4s内的位移为零.
(5)前5s内的位移为:${x}_{5}={v}_{0}{t}_{5}+\frac{1}{2}a{{t}_{5}}^{2}$=$20×5-\frac{1}{2}×10×25m=-25m$,负号表示位移的方向向下.
答:(1)小球离开平台上升的最大高度为20m,用了2s时间.
(2)第2秒内上升的高度为5m,一秒内的平均速度为5m/s,前两秒内的平均速度为10m/s.
(3)前三秒内走的位移为15m.
(4)前四秒内走的位移为0.
(5)前五秒内走的位移为-25m.
点评 解决本题的关键掌握处理竖直上抛运动的方法,可以全过程分析研究,也可以分为上升和下降过程分析研究.

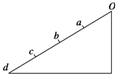 如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d四个位置,下列说法正确的是( )
如图所示,光滑斜面上的四段距离相等,质点从O点由静止开始下滑,做匀加速直线运动,先后通过a、b、c、d四个位置,下列说法正确的是( )| A. | 质点由O到达各点的时间之比ta:tb:tc:td=1:$\sqrt{2}$:$\sqrt{3}$:2 | |
| B. | 质点通过各点的速率之比va:vb:vc:vd=1:2:3:4 | |
| C. | 在斜面上运动的平均速度$\overline{v}$=vb | |
| D. | 在斜面上运动的平均速度$\overline{v}$=$\frac{{v}_{d}}{2}$ |
| A. | 温度越高,液体的饱和汽压越大 | |
| B. | 温度相同的氢气和氧气,分子的平均速率相同 | |
| C. | 空气相对湿度越大时,空气中水蒸气压强越接近饱和汽压,水蒸发越慢 | |
| D. | 布朗运动和扩散现象都能在气体、液体、固体中发生 |
| A. | 近地卫星的环绕速率可以大于7.9km/s,但发射速度不能小于7.9km/s | |
| B. | 地球同步卫星相对地球是静止的,可以固定对一个区域拍照 | |
| C. | 近地卫星和地球同步卫星,可能具有相同的速率 | |
| D. | 若近地卫星和地球同步卫星质量相同,近地卫星的机械能较大 |
| A. | 刘翔在110米栏比赛过程中做匀加速直线运动 | |
| B. | 110m是刘翔比赛中位移时的大小 | |
| C. | 刘翔比赛中的平均速度约是8.3m/s | |
| D. | 6.0m/s指刘翔比赛中的瞬时速度 |
 如图所示,虚线OC与y轴的夹角θ=60°,在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场.虚线OC与x轴所夹范围内有一沿x轴正方向、电场强度大小为E的匀强电场.一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M(0,L)沿x轴的正方向射入磁场中.要使粒子a从OC边界离开磁场后竖直向下垂直进入匀强电场,经过匀强电场后从x轴上的P点(图中未画出)离开,则:
如图所示,虚线OC与y轴的夹角θ=60°,在此角范围内有一方向垂直于xOy平面向外、磁感应强度大小为B的匀强磁场.虚线OC与x轴所夹范围内有一沿x轴正方向、电场强度大小为E的匀强电场.一质量为m、电荷量为q的带正电的粒子a(不计重力)从y轴的点M(0,L)沿x轴的正方向射入磁场中.要使粒子a从OC边界离开磁场后竖直向下垂直进入匀强电场,经过匀强电场后从x轴上的P点(图中未画出)离开,则: 如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=600nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的$\sqrt{2}$倍,且与MN所成的夹角α=30°.求:
如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=600nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的$\sqrt{2}$倍,且与MN所成的夹角α=30°.求:
