题目内容
6. 如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=600nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的$\sqrt{2}$倍,且与MN所成的夹角α=30°.求:
如图所示,MN是一条通过透明球体球心的直线,在真空中波长为λ0=600nm的单色细光束AB平行于MN射向球体,B为入射点,若出射光线CD与MN的交点P到球心O的距离是球半径的$\sqrt{2}$倍,且与MN所成的夹角α=30°.求:①透明体的折射率n;
②此单色光在透明球体中的波长λ.
分析 ①连接OB、BC,在B点光线的入射角、折射角分别标为i、r,作出光路图,根据几何关系求出入射角与折射角,根据折射定律求解折射率n.
②根据波速、波长、频率的关系即可求得此单色光在透明球体中的波长.
解答  解:①连接OB、BC,作出光路图.在B点光线的入射角、折射角分别标为i、r,如图所示.
解:①连接OB、BC,作出光路图.在B点光线的入射角、折射角分别标为i、r,如图所示.
在△OCP中:有:$\frac{OC}{sinα}$=$\frac{OP}{sin∠OCP}$
据题:OP=$\sqrt{2}$OC,α=30°
解得:∠OCP=135°(45°值舍去)
进而可得:∠COP=15°
由折射率定义:在B点有:n=$\frac{sini}{sinr}$
在C点有:n=$\frac{sin(180°-135°)}{sin∠BCO}$
又∠BCO=r
所以,i=45°
又:∠BOC=180°-i-∠COP=120°
故:r=30°
因此,透明体的折射率 n=$\frac{sini}{sinr}$=$\frac{sin45°}{sin30°}$=$\sqrt{2}$
②由n=$\frac{c}{v}$=$\frac{{λ}_{0}f}{λf}$=$\frac{{λ}_{0}}{λ}$
得:λ=$\frac{{λ}_{0}}{n}$=424nm
答:①透明体的折射率n为 $\sqrt{2}$;
②此单色光在透明球体中的波长λ为424nm
点评 本题是较为复杂的几何光学问题,其基础是作出光路图,根据几何知识确定入射角与折射角,根据折射定律求解,折射过程中频率不变.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.分析下列物理现象:①“闻其声而不见其人”; ②夏天里在一次闪电过后,有时雷声轰鸣不绝;③当正在鸣笛的火车向着我们急驶而来时,我们听到汽笛声的音调变高;④围绕振动的音叉转一圈会听到忽强忽弱的声音.这些物理现象分别属于波的( )
| A. | 衍射、折射、干涉、多普勒效应 | B. | 折射、反射、干涉、多普勒效应 | ||
| C. | 衍射、反射、多普勒效应、干涉 | D. | 折射、衍射、多普勒效应、干涉 |
1.在伽利略的斜面实验中,小球停下来的高度为h1,与它出发时的高度h2相同,我们把这一事实说成是“某个量是守恒的”,下列说法中正确的是( )
| A. | 小球在运动的过程中速度是守恒的 | B. | 小球在运动的过程中高度是守恒的 | ||
| C. | 小球在运动的过程中动能是守恒的 | D. | 小球在运动的过程中能量是守恒的 |
13.如图,小车在水平面上做匀速运动.以下几对力中属于相互作用力的是( )


| A. | 小车的重力和水平面的支持力 | |
| B. | 推力F和小车受到的摩擦力 | |
| C. | 小车受到的支持力和小车对水平面的压力 | |
| D. | 小车的重力和小车对水平面的压力 |
 在“验证力的平行四边形定则”的实验中,实验装置如图所示.
在“验证力的平行四边形定则”的实验中,实验装置如图所示. 小杨同学用台秤研究他在电梯中的超失重现象.他在地面上用台秤称得其体重为500N,再将台秤移至 电梯内称其体重.电梯从t=0时由静止开始运动,到t=11s时停止,得到台秤的示数F随时间t变化的图象如图所示.g=10m/s2.
小杨同学用台秤研究他在电梯中的超失重现象.他在地面上用台秤称得其体重为500N,再将台秤移至 电梯内称其体重.电梯从t=0时由静止开始运动,到t=11s时停止,得到台秤的示数F随时间t变化的图象如图所示.g=10m/s2. 如图,一个质子在经U=5000V的加速电压加速后,在距两极板等距离处垂直进入平行板间的匀强电场,若两极板间距离d=1.0cm,板长L=5.0cm,那么,要使质子能从平行板间飞出,求:
如图,一个质子在经U=5000V的加速电压加速后,在距两极板等距离处垂直进入平行板间的匀强电场,若两极板间距离d=1.0cm,板长L=5.0cm,那么,要使质子能从平行板间飞出,求: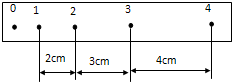 在《研究匀变速直线运动》的实验中得到一部分纸带如图所示,取相邻的两计数点的时间间隔为0.1s,则物体的加速度是1m/s2,1到3两点间运动的平均速度是0.25m/s.
在《研究匀变速直线运动》的实验中得到一部分纸带如图所示,取相邻的两计数点的时间间隔为0.1s,则物体的加速度是1m/s2,1到3两点间运动的平均速度是0.25m/s.