题目内容
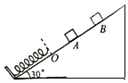
【题目】如图,平行板电容器的Ⅳ板开有一小孔,与固定圆筒的小孔a正对,O是圆筒的圆心,圆筒的内径为r,筒内有垂直纸面的匀强磁场,筒壁光滑.电容器内紧靠极板肘有一个带电粒子(初速度为零),经电压U加速后从a孔垂直磁场并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞三次后恰好又从小孔a射出.带电粒子每次与筒壁发生碰撞时电荷量和动能都不损失,粒子的比荷为q/m=k不计粒子的重力和空气阻力.求

(1)带电粒子进入磁场的速度大小?
(2)筒内磁感应强度B的大小?(结论均用r、E,和k表示)
【答案】(1)![]() (2)
(2) ![]()
【解析】(1)由动能定理:![]()
得:![]() ;
;
(2)带电粒子在磁场中作匀速圆周运动,由于带电粒子与圆筒壁碰撞时无电量和动能损失,故每次碰撞前后粒子速度大小不变。设圆周运动的半径为R,由牛顿第二定律得:![]()
速度方向总是沿着圆筒半径方向,3个碰撞点与小孔a恰好将圆筒壁四等分,粒子在圆筒内的轨迹具有对称性,由四段相同的圆弧组成,则每段轨迹圆弧对应的圆心角为90°,则由几何关系得:R=r
联立解得: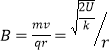 。
。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目