��Ŀ����
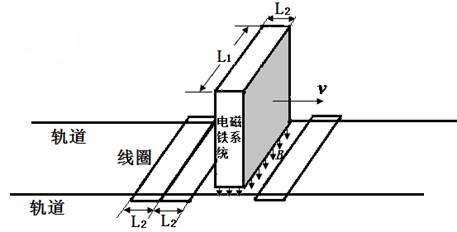
�����ƶ��Ǵ������г��ڸ�������ʱ�����ƶ���һ�ַ�ʽ��ij�о������Ƴɵij����ģ��������ģ��������г��������ƶ����̣���ͼ��ʾ��ģ�ͳ��ij����¶˰�װ�е����ϵͳ�������ϵͳ�������·���ˮƽ��������ΪL1���еij�ΪL1����ΪL2�ľ��������ڲ�����ǿ�ų����ôų��ĴŸ�Ӧǿ�ȴ�СΪB��������ֱ���£���������L1����ΪL2�ĵ��Ѿ�����Ȧ�ȼ�������ڹ�������룬����ҲΪL2��ÿ����Ȧ�ĵ���ΪR�����ߴ�ϸ���Բ��ƣ���ij��ʵ���У��������ϵͳ��ʼ�ƶ������ϵͳ�պ�����������n����Ȧ����֪ģ�ͳ���������Ϊm�������������ƣ���
��1���ڵ����ϵͳ�Ĵų�ȫ����������һ����Ȧ�Ĺ����У�ͨ����Ȧ�ĵ����q��
��2����ɲ�������У���Ȧ���������ܵ���Q��
��3�������ϵͳ�ս����k��k��n������Ȧʱ����Ȧ�еĵ繦��P��

��1���ڵ����ϵͳ�Ĵų�ȫ����������һ����Ȧ�Ĺ����У�ͨ����Ȧ�ĵ����q��
��2����ɲ�������У���Ȧ���������ܵ���Q��
��3�������ϵͳ�ս����k��k��n������Ȧʱ����Ȧ�еĵ繦��P��

��������1�����ݷ����ڵ�Ÿ�Ӧ���ɺͱպϵ�·ŷķ�������ƽ�������Ĵ�С������q=It���ͨ���ĵ�����
��2������ţ�ٵڶ����ɡ���������ʽ���и�����ĸ�Ӧ�綯�ƹ�ʽ�ͱպϵ�·ŷķ���ɣ������ֵķ���������ٶȵĴ�С���ٸ��������غ㶨�������Ȧ���������ܵ��ȣ�
��3�������ַ�������ٶȱ仯�����ó������ϵͳ�ս����k��k��n������Ȧʱ�ٶȵı仯�����Ӷ������ʱ���ٶȴ�С���Ӷ�����P=
�����Ȧ�еĵ繦��
��2������ţ�ٵڶ����ɡ���������ʽ���и�����ĸ�Ӧ�綯�ƹ�ʽ�ͱպϵ�·ŷķ���ɣ������ֵķ���������ٶȵĴ�С���ٸ��������غ㶨�������Ȧ���������ܵ��ȣ�
��3�������ַ�������ٶȱ仯�����ó������ϵͳ�ս����k��k��n������Ȧʱ�ٶȵı仯�����Ӷ������ʱ���ٶȴ�С���Ӷ�����P=
| (BL1vk-1)2 |
| R |
����⣺��1���ڵ��ϵͳ�����߿��Ϸ���t�Ĺ����У��߿��в�����ƽ����Ӧ�綯��
=
ƽ������
=
�߿�ĵ����q=
��t=
��
��2�����ϵͳ���߿��Ϸ���һʱ�����ٶ�v�˶�ʱ������һ��L1���ڴų����и�Ÿ����˶�����������ܵ��߿����õ���������С�����߿����ܵİ�������
F=BIL1��I=
��F=
����ϵͳ�����˶�ʱ��˲ʱ���ٶ�a=
��
�������̵�ʱ���t���ٶȼ�С��v���˶���λ�ơ�x
a��t=
��t��
����v=
��v=
��x
����v0=
2nL2������v0Ϊ��ʼɲ��ʱ�ij��ٶ�
�������غ㶨��֪���߿��в�����������Q=
mv02
����ã�Q=
��
��3��������մ����ڣ�k-1�����ų�����ʱ���ٶ�Ϊvk-1��
v0-vk-1=
?2(k-1)L2
��vk-1=
?2(n-k+1)L2
��Ȧ�ĵ繦��P=
��P=
?4(n-k+1)2L22��
�𣺣�1���ڵ����ϵͳ�Ĵų�ȫ����������һ����Ȧ�Ĺ����У�ͨ����Ȧ�ĵ����Ϊ
��
��2����ɲ�������У���Ȧ���������ܵ���Ϊ
��
��3����Ȧ�еĵ繦��
?4(n-k+1)2L22��
. |
| E |
| Bl1l2 |
| ��t |
ƽ������
. |
| I |
| ||
| R |
�߿�ĵ����q=
. |
| I |
| BL1L2 |
| R |
��2�����ϵͳ���߿��Ϸ���һʱ�����ٶ�v�˶�ʱ������һ��L1���ڴų����и�Ÿ����˶�����������ܵ��߿����õ���������С�����߿����ܵİ�������
F=BIL1��I=
| BLv1 |
| R |
| B2L2v1 |
| R |
����ϵͳ�����˶�ʱ��˲ʱ���ٶ�a=
| B2L12v |
| mR |
�������̵�ʱ���t���ٶȼ�С��v���˶���λ�ơ�x
a��t=
| B2L12v |
| mR |
����v=
| B2L12��x |
| mR |
 |
| B2L12 |
| mR |
 |
����v0=
| B2L12 |
| mR |
�������غ㶨��֪���߿��в�����������Q=
| 1 |
| 2 |
����ã�Q=
| 2B4L14n2L22 |
| mR2 |
��3��������մ����ڣ�k-1�����ų�����ʱ���ٶ�Ϊvk-1��
v0-vk-1=
| B2L12 |
| mR |
��vk-1=
| B2L12 |
| mR |
��Ȧ�ĵ繦��P=
| (BL1vk-1)2 |
| R |
��P=
| B6L16 |
| m2R3 |
�𣺣�1���ڵ����ϵͳ�Ĵų�ȫ����������һ����Ȧ�Ĺ����У�ͨ����Ȧ�ĵ����Ϊ
| BL1L2 |
| R |
��2����ɲ�������У���Ȧ���������ܵ���Ϊ
| 2B4L14n2L22 |
| mR2 |
��3����Ȧ�еĵ繦��
| B6L16 |
| m2R3 |
���������������龳���£������dz�������ģ�ͣ������ڴų�������Ȧ�ڶ������ͣ���2����3���ʶ�ѧ��������Ҫ��ϸߣ�������ֵ�˼����н����

��ϰ��ϵ�д�
�����Ŀ
 �����ƶ��Ǵ������г��ڸ�������ʱ�����ƶ���һ�ַ�ʽ��ij�о����Ƴ���ͼ��ʾ�ij����ģ��������ģ��������г��������ƶ����̣������¶˰�װ�е����ϵͳ�����ڳ�ΪL1=0.6m����L2=0.2m�ľ��������ڲ�����ֱ�������ǿ�ų����Ÿ�Ӧǿ�ȿ��泵�ٵļ�С���Զ������ɳ����ٶȴ��������ƣ����������B1=2T����������L1����ҲΪL2�ĵ��Ѿ�����Ȧ����������ڹ�������룬����ҲΪL2��ÿ����Ȧ�ĵ���ΪR1=0.1�������ߴ�ϸ���Բ��ƣ���ij��ʵ���У�ģ�ͳ��ٶ�Ϊv0=20m/sʱ�����������ϵͳ��ʼ�ƶ����������Լ��ٶ�a1=2m/s2���ȼ���ֱ���˶������Ÿ�Ӧǿ�����ӵ�B1ʱ�ͱ��ֲ��䣬ֱ��ģ�ͳ�ֹͣ�˶�����֪ģ�ͳ���������Ϊm1=36kg�������������ƣ������ǴŸ�Ӧǿ�ȵı仯����ĵ�Ÿ�Ӧ�����Լ���Ȧ�����Ĵų��Ե���������ų���Ӱ�죮
�����ƶ��Ǵ������г��ڸ�������ʱ�����ƶ���һ�ַ�ʽ��ij�о����Ƴ���ͼ��ʾ�ij����ģ��������ģ��������г��������ƶ����̣������¶˰�װ�е����ϵͳ�����ڳ�ΪL1=0.6m����L2=0.2m�ľ��������ڲ�����ֱ�������ǿ�ų����Ÿ�Ӧǿ�ȿ��泵�ٵļ�С���Զ������ɳ����ٶȴ��������ƣ����������B1=2T����������L1����ҲΪL2�ĵ��Ѿ�����Ȧ����������ڹ�������룬����ҲΪL2��ÿ����Ȧ�ĵ���ΪR1=0.1�������ߴ�ϸ���Բ��ƣ���ij��ʵ���У�ģ�ͳ��ٶ�Ϊv0=20m/sʱ�����������ϵͳ��ʼ�ƶ����������Լ��ٶ�a1=2m/s2���ȼ���ֱ���˶������Ÿ�Ӧǿ�����ӵ�B1ʱ�ͱ��ֲ��䣬ֱ��ģ�ͳ�ֹͣ�˶�����֪ģ�ͳ���������Ϊm1=36kg�������������ƣ������ǴŸ�Ӧǿ�ȵı仯����ĵ�Ÿ�Ӧ�����Լ���Ȧ�����Ĵų��Ե���������ų���Ӱ�죮