题目内容
15.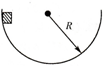 质量为m的物体沿着半径为R的半球金属球壳滑到最低点时的速度大小为v,如图所示.若物体与球壳之间的摩擦因数为μ,则物体在最低点时的( )
质量为m的物体沿着半径为R的半球金属球壳滑到最低点时的速度大小为v,如图所示.若物体与球壳之间的摩擦因数为μ,则物体在最低点时的( )| A. | 向心加速度为$\frac{{v}^{2}}{R}$ | B. | 向心力为m(g+$\frac{{v}^{2}}{R}$) | ||
| C. | 对球壳的压力为$\frac{m{v}^{2}}{R}$ | D. | 受到的摩擦力为μm(g+$\frac{{v}^{2}}{R}$) |
分析 根据向心加速度和向心力的公式求出向心加速度大小和向心力的大小,根据牛顿第二定律求出支持力的大小,从而得出滑动摩擦力的大小.
解答 解:A、向心加速度的大小a=$\frac{{v}^{2}}{R}$,故A正确.
B、向心力${F}_{n}=\frac{{v}^{2}}{R}$,故B错误.
C、根据牛顿第二定律得,N-mg=m$\frac{{v}^{2}}{R}$,解得N=mg+m$\frac{{v}^{2}}{R}$,则物体对球壳的压力为$mg+m\frac{{v}^{2}}{R}$,故C错误.
D、物体所受的摩擦力f=μN=μm(g+$\frac{{v}^{2}}{R}$).故D正确.
故选:AD
点评 解决本题的关键知道 物体做圆周运动的向心力来源,结合牛顿第二定律进行求解,基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.关于质点做匀速圆周运动,下列说法中正确的是( )
| A. | 质点的速度不变 | B. | 质点的周期不变 | ||
| C. | 质点的角速度不变 | D. | 质点的加速度不变 |
3.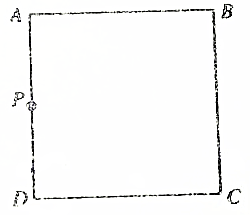 如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )
如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )
 如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )
如图所示,一匀强电场平行于正方形区域ABCD,AB边水平,BC边垂直,A、B、C三点的电势分别为6V、2V、-2V.一质量为m,电量大小为q的带电微粒,从P点射入该电场区,恰好沿水平直线运动,下列判断正确的是( )| A. | 微粒带正电 | B. | 微粒做匀速直线运动 | ||
| C. | 电场强度的大小为$\frac{\sqrt{2}mg}{q}$ | D. | 微粒的电势能逐渐减少 |
3.某物理兴趣小组先用伏安法来测定一干电池的电动势和内电阻.现有以下器材可供选用:
A.电流计G1(量程3.0mA,内阻Rg=10Ω)
B.电流计G2(量程5.0mA,内阻约为1Ω)
C.电流表A(量程0.6A,内阻约为0.50Ω)
D.滑动变阻器R1(0~20Ω,10A)
E.电阻箱R2
F.开关S和导线若干
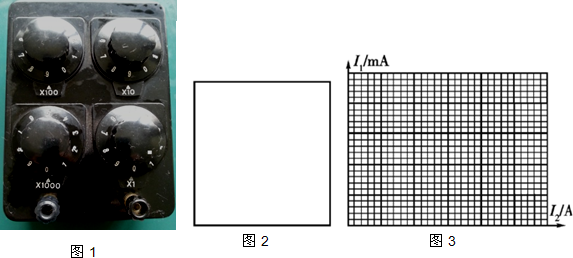
(1)实验小组先用电流计和电阻箱通过改装成一个电压表,则电流计应选用G1.(填G1或G2).所用的电阻箱阻值如图1所示,读数是990Ω.
(2)请在图2线框内画出该实验小组所采用的实验电路图.(标注所选择的器材符号)
(3)该小组在(1)、(2)的基础上根据实验设计的电路图测得的数据如表,请你在图3坐标纸上选择合理的标度,并作出相应的图线.
(4)根据(3)中的图线求得电源的电动势E=1.48V(保留三位有效数字),电源的内阻r=0.84Ω(保留两位有效数字)
A.电流计G1(量程3.0mA,内阻Rg=10Ω)
B.电流计G2(量程5.0mA,内阻约为1Ω)
C.电流表A(量程0.6A,内阻约为0.50Ω)
D.滑动变阻器R1(0~20Ω,10A)
E.电阻箱R2
F.开关S和导线若干

(1)实验小组先用电流计和电阻箱通过改装成一个电压表,则电流计应选用G1.(填G1或G2).所用的电阻箱阻值如图1所示,读数是990Ω.
(2)请在图2线框内画出该实验小组所采用的实验电路图.(标注所选择的器材符号)
(3)该小组在(1)、(2)的基础上根据实验设计的电路图测得的数据如表,请你在图3坐标纸上选择合理的标度,并作出相应的图线.
| 序 号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 电流表G(I1/mA) | 1.36 | 1.34 | 1.26 | 1.24 | 1.18 | 1.12 |
| 电流表A(I2/A) | 0.12 | 0.16 | 0.20 | 0.28 | 0.36 | 0.44 |
10.关于重力做功和重力势能,下列说法中正确的是( )
| A. | 当重力做正功时,物体的重力势能可能不变 | |
| B. | 当物体克服重力做功时,物体的质量势能一定减小 | |
| C. | 重力势能为负值时,说明其方向与规定的正方向相反 | |
| D. | 重力势能的大小与零势能参考面的选取有关 |
20.布朗运动是说明分子运动的重要实验事实,关于布朗运动,下列说法中正确的是( )
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 布朗运动是悬浮在液体中的固体分子的无规则运动 | |
| C. | 布朗运动产生的原因是液体分子对小颗粒碰撞时产生的作用力不平衡引起的 | |
| D. | 悬浮的小颗粒越大,撞击它的分子数越多,布朗运动越剧烈 |
7.关于晶体和非晶体,下列说法中正确的是( )
| A. | 具有规则几何外形的物体一定单晶体 | |
| B. | 非晶体一定没有固定的熔点 | |
| C. | 晶体的物理性质一定表现为各向异性 | |
| D. | 天然水晶和普通玻璃都是透明的,故它们都是晶体 |
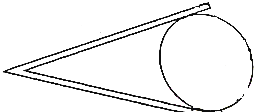 如图所示,两杆的一端有轴相连,构成一个夹子.用架子夹一个半径为R的球,夹子与球面间的动摩擦因数为μ,可以认为它们之间的最大静摩擦力等于滑动摩擦力,已知球放在光滑水平面上,杆的重力忽略不计.那么,要想用这个夹子把球夹住而不向前滚动,杆至少多长?
如图所示,两杆的一端有轴相连,构成一个夹子.用架子夹一个半径为R的球,夹子与球面间的动摩擦因数为μ,可以认为它们之间的最大静摩擦力等于滑动摩擦力,已知球放在光滑水平面上,杆的重力忽略不计.那么,要想用这个夹子把球夹住而不向前滚动,杆至少多长? 文文和新新用相同大小的力提着重为100N的水桶在水平路面上行走,他们提桶的力的合力大小为100 N,合力的方向竖直向上(填“竖直向上”或“竖直向下”),提桶的手臂间的夹角越小(填“大”或“小”)越省力.
文文和新新用相同大小的力提着重为100N的水桶在水平路面上行走,他们提桶的力的合力大小为100 N,合力的方向竖直向上(填“竖直向上”或“竖直向下”),提桶的手臂间的夹角越小(填“大”或“小”)越省力.