题目内容
12．
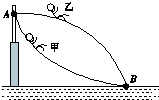如图，游乐场中，从高处A到水面B处有两条长度相同的光滑轨道．甲、乙两小孩沿不同轨道同时从A处自由滑向B处，下列说法正确的有（ ）| A． | 甲、乙在同一高度的速度大小相等 | B． | 甲的切向加速度始终比乙的大 | ||
| C． | 乙比甲先到达B处 | D． | 甲比乙先到达B处 |
分析 ①由受力分析及牛顿第二定律可知，甲的切向加速度先比乙的大，后比乙的小；
②可以使用机械能守恒来说明，也可以使用运动学的公式计算，后一种方法比较麻烦；
③哪一个先达到B点，可以通过速度的变化快慢来理解，也可以使用v-t图象来计算说明．
解答 解：A、由机械能守恒定律可知，各点的机械能保持不变，高度（重力势能）相等处的动能也相等，故A正确；
B、由受力分析及牛顿第二定律可知，甲的切向加速度先比乙的大，后比乙的小，故B错误；
C、D、甲的切向加速度先比乙的大，速度增大的比较快，开始阶段的位移比较大，故甲总是先达到同一高度的位置．故C错误，D正确．
故选：AD
点评 本题应该用“加速度”解释：高度相同，到达底端的速度大小就相同，但甲的加速度逐渐减小，乙的加速度逐渐增大．所以它们的速度增加的快慢不同，甲增加得最快，乙增加得最慢．
练习册系列答案
相关题目
2．关于电容器和电容，以下说法正确的是（ ）
| A． | 电容器充电后，两极板总带等量异种电荷 | |
| B． | 电容器的带电量是两极板带电量之和 | |
| C． | 电容器电容的大小与其带电量及两极板间电势差有关 | |
| D． | 电容器两极板间电势差每增加1V，电容器的电容即增加1F |
3．下面能正确表示物体做匀加速直线运动的图象是（ ）
| A． |  | B． |  | C． |  | D． |  |
20．下列关于物体的速度、加速度、速度变化量的说法正确的是（ ）
| A． | 加速度等于0，速度一定等于0 | |
| B． | 速度变化量较大，加速度可能较小 | |
| C． | 加速度方向向东，速度方向可能向西 | |
| D． | 加速度变小，速度可能变大 |
7．电流表的内阻是Rg=200Ω，满刻度电流值是Ig=500 μA，现欲把这电流表改装成量程为2.0V的电压表，正确的方法是（ ）
| A． | 应串联一个0.05Ω的电阻 | B． | 应并联一个0.05Ω的电阻 | ||
| C． | 应串联一个3 800Ω的电阻 | D． | 应并联一个3 800Ω的电阻 |
17．
如图所示，L1、L2、L3是完全相同的灯泡，L为直流电阻可忽略的自感线圈，开关S原来接通，当开关S断开时，下面说法正确的是（考虑电源内阻）（ ）
如图所示，L1、L2、L3是完全相同的灯泡，L为直流电阻可忽略的自感线圈，开关S原来接通，当开关S断开时，下面说法正确的是（考虑电源内阻）（ ）| A． | L1立即变亮 | B． | L2闪亮一下后恢复原来的亮度 | ||
| C． | L3变暗一下后恢复原来的亮度 | D． | L3闪亮一下后恢复原来的亮度 |
4．下列关于摩擦力的说法，正确的是（ ）
| A． | 相互挤压的粗糙物体之间一定有摩擦力存在 | |
| B． | 运动的物体之间一定存在摩擦力 | |
| C． | 运动的物体之间一定不存在静摩擦力 | |
| D． | 只有相互挤动或相对运动趋势的粗糙物体之间才有摩擦力的作用 |
1．质量为m的物体在几个恒力的作用下以速度v0在水平面上做匀速运动，若撇去其中一个力F0，从此时开始计时，则有（ ）
| A． | 物体运动的轨迹可能是圆 | |
| B． | 物体的速度与合力之前的夹角一定不断改变 | |
| C． | t时刻物体的速度大小等于$\sqrt{{{v}_{0}}^{2}+{{F}_{0}}^{2}/{m}^{2}}$ | |
| D． | 在相等的时间内物体的速度变化量一定相等 |
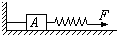如图所示，放在水平地面上的物体A 重G=100N，左侧用轻质绳系在墙上，此时张力为零，右侧连着一轻质弹簧，已知物体与地面间的动摩擦因数μ=0.4，可认为物体所受的最大静摩擦力等于滑动摩擦力．弹簧的劲度系数k=2500N/m．在弹簧的右端加一水平拉力 F，则：