Question

【题目】如图所示，在空间中存在垂直纸面向外，宽度为d的有界匀强磁场．一质量为m、带电荷量为q的粒子自下边界的P点处以速度v沿与下边界成θ=30°角的方向垂直射入磁场，恰能垂直于上边界射出，不计粒子重力，题中d、m、q、v均为已知量．则

（1）粒子带何种电荷？
（2）磁场磁感应强度为多少？

Answer 1

【答案】
（1）解：粒子在磁场中运动轨迹如图所示，粒子向上偏转，由左手定则可判断粒子带正电．

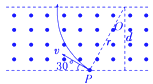
（2）解：粒子在磁场中运动轨迹如图所示，设圆周运动半径为r，

由几何关系可得：rcos 30°=d

由洛伦兹力提供向心力得：

qvB=m

由以上两式可解得：B= ；

答：磁场磁感应强度为B= ．

【解析】根据粒子偏转方向结合左手定则判断粒子的电性；

画出轨迹，由几何知识确定半径，然后由牛顿第二定律列方程求B的大小．

【考点精析】解答此题的关键在于理解洛伦兹力的相关知识，掌握洛伦兹力始终垂直于v的方向，所以洛伦兹力一定不做功，以及对感应电流的方向的理解，了解通电导体在磁场中受力方向：跟电流方向和磁感线方向有关．（左手定则）．