题目内容
11. 如图所示,在E=103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨道QPN与一水平绝缘轨道MN在N点平滑相接,半圆形轨道平面与电场线平行,其半径R=40cm,N为半圆形轨道最低点,P为QN圆弧的中点,一带负电的小滑块质量m=10g,电荷量q=10-4C与水平轨道间的动摩擦因数μ=0.15,位于N点右侧1.5m的M点处,取g=10m/s2.求:
如图所示,在E=103V/m的竖直匀强电场中,有一光滑的半圆形绝缘轨道QPN与一水平绝缘轨道MN在N点平滑相接,半圆形轨道平面与电场线平行,其半径R=40cm,N为半圆形轨道最低点,P为QN圆弧的中点,一带负电的小滑块质量m=10g,电荷量q=10-4C与水平轨道间的动摩擦因数μ=0.15,位于N点右侧1.5m的M点处,取g=10m/s2.求:(1)要使小滑块恰能运动到圆轨道的最高点Q,则滑块应从M点以多大的初速度v0向左运动?
(2)这样运动的滑块通过P点时受到轨道的压力是多大?
分析 (1)小球恰能通过最高点,在最高点重力和电场力的合力提供向心力,根据向心力公式求得最高点速度,再对从M到N过程运用动能定理列式求初速度;
(2)先对从M到P过程运用动能定理求得P点速度,在P点支持力提供向心力,根据向心力公式列式求解.
解答 解:(1)设滑块到达Q点时速度为v,
则由牛顿第二定律得:mg+qE=m$\frac{{v}^{2}}{R}$,
滑块从开始运动至到达Q点过程中,由动能定理得:
-mg•2R-qE•2R-μ(mg+qE)x=$\frac{1}{2}$mv2-$\frac{1}{2}$mv${\;}_{0}^{2}$
联立方程组,解得:v0=7m/s;
(2)设滑块到达P点时速度为v′,则从开始运动至到达P点过程中,
由动能定理得:-(mg+qE)R-μ(qE+mg)x=$\frac{1}{2}$mv′2-$\frac{1}{2}$mv${\;}_{0}^{2}$
又在P点时,由牛顿第二定律得:FN=m$\frac{v{′}^{2}}{R}$,
代入数据解得:FN=0.6N,方向水平向右;
答:(1)要使小滑块恰能运动到圆轨道的最高点Q,则滑块应从M点以7m/s的初速度v0向左运动;
(2)这样运动的滑块通过P点时受到轨道的压力是0.6N,方向水平向右.
点评 此题中滑块恰好通过最高点时轨道对滑块没有弹力,由牛顿定律求出临界速度,再根据动能定理和牛顿运定律结合求解小球对轨道的弹力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
1. 如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电荷以初速度v0,方向与电流方向同相运动,以后该电荷可能将( )
如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电荷以初速度v0,方向与电流方向同相运动,以后该电荷可能将( )
 如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电荷以初速度v0,方向与电流方向同相运动,以后该电荷可能将( )
如图所示,水平直导线中通有稳恒电流I,导线的正上方处有一电荷以初速度v0,方向与电流方向同相运动,以后该电荷可能将( )| A. | 沿路径a运动,曲率半径变小 | B. | 沿路径a运动,曲率半径变大 | ||
| C. | 沿路径b运动,曲率半径变小 | D. | 沿路径b运动,曲率半径变大 |
2.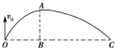 将一小球在O处竖直向上抛出,小球在空中运动过程中始终受大小不变的水平风力的作用,A为轨迹上的最高点,轨迹上的C点与O点在同一水平面上,A、B连线与OC垂直,下列说法中正确的是( )
将一小球在O处竖直向上抛出,小球在空中运动过程中始终受大小不变的水平风力的作用,A为轨迹上的最高点,轨迹上的C点与O点在同一水平面上,A、B连线与OC垂直,下列说法中正确的是( )
 将一小球在O处竖直向上抛出,小球在空中运动过程中始终受大小不变的水平风力的作用,A为轨迹上的最高点,轨迹上的C点与O点在同一水平面上,A、B连线与OC垂直,下列说法中正确的是( )
将一小球在O处竖直向上抛出,小球在空中运动过程中始终受大小不变的水平风力的作用,A为轨迹上的最高点,轨迹上的C点与O点在同一水平面上,A、B连线与OC垂直,下列说法中正确的是( )| A. | 小球从O到A的时间与从A到C的时间相等 | |
| B. | 小球在运动过程中任意相等时间内速度变化量大小相等,方向相同 | |
| C. | 小球在运动过程中做变加速运动 | |
| D. | BC段的长度为OB段长度的两倍 |
19.某交流发电机给灯泡供电,产生正弦式交变电流的图象如图所示,下列说法中正确的是( )


| A. | 交变电流的频率为0.05Hz | |
| B. | 交变电流的瞬时表达式为i=5cos50πt(A) | |
| C. | 在t=0.015s时,穿过交流发电机线圈的磁通量为零 | |
| D. | 若发电机线圈电阻为0.8Ω,则其产生的热功率为10W |
16.下面涉及运动概念的几个说法,正确的是( )
| A. | “我们要珍惜每一分每一秒”中的“一秒”指的是时刻 | |
| B. | “位移”大小总是等于路程大小,方向由初位置指向末位置 | |
| C. | 旅游大巴以36km/h的速度通过某座大桥,这个速度是“平均速度” | |
| D. | 花样滑冰运动员正在表演冰上舞蹈运作,此时该运动员可以看作质点 |
20.天文学家发现了某恒星有一颗行星在圆形轨道上绕其运动,并测出了行星的轨道半径和运行周期,由此可推算出( )
| A. | 行星的半径 | B. | 恒星的半径 | C. | 行星的质量 | D. | 恒星的质量 |
1.假设有一列车以接近于光速的速度运动,车窗沿运动方向为长,垂直运动方向为宽,根据相对论的知识,站在地面上的人观测到( )
| A. | 车窗的宽度比静止时更宽 | B. | 车窗的宽度比静止时更窄 | ||
| C. | 车窗的长度比静止时更长 | D. | 车窗的长度比静止时更短 |
 如图所示,相距L足够长的两根平行金属导轨与水平面成θ角,导轨电阻不计,上端连接阻值为R的电阻,在距导轨上端d1处放置一水平导体棒ab,其质量为m,电阻也为R,导轨对导体棒ab的滑动摩擦力等于mgsinθ (最大静摩擦力始终等于滑动摩擦力).整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.
如图所示,相距L足够长的两根平行金属导轨与水平面成θ角,导轨电阻不计,上端连接阻值为R的电阻,在距导轨上端d1处放置一水平导体棒ab,其质量为m,电阻也为R,导轨对导体棒ab的滑动摩擦力等于mgsinθ (最大静摩擦力始终等于滑动摩擦力).整个装置处于匀强磁场中,磁场的方向垂直导轨平面向上.