题目内容
【题目】如图所示,斜面ABC下端与光滑的圆弧轨道CDE相切于C,整个装置竖直固定,D是最低点,圆心角∠DOC=37°,E、B与圆心O等高,圆弧轨道半径R=0.30m,斜面长L=1.90m,AB部分光滑,BC部分粗糙。现有一个质量m=0.10kg的小物块P从斜面上端A点无初速下滑,物块P与斜面BC部分之间的动摩擦因数μ=0.75.取sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2,忽略空气阻力。求:
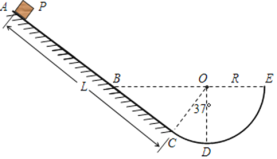
(1)物块第一次通过C点时的速度大小vC。
(2)物块第一次通过D点时受到轨道的支持力大小FD。
(3)物块最终所处的位置。
【答案】(1)![]() (2)7.4N(3)0.35m
(2)7.4N(3)0.35m
【解析】
由题中“斜面ABC下端与光滑的圆弧轨道CDE相切于C”可知,本题考查动能定理、圆周运动和机械能守恒,根据过程分析,运用动能定理、机械能守恒和牛顿第二定律可以解答。
(1)BC长度![]() ,由动能定理可得
,由动能定理可得
![]()
代入数据的
![]()
物块在BC部分所受的摩擦力大小为
![]()
所受合力为
![]()
故
![]()
(2)设物块第一次通过D点的速度为![]() ,由动能定理得
,由动能定理得
![]()
有牛顿第二定律得
![]()
联立解得
![]()
(3)物块每次通过BC所损失的机械能为
![]()
物块在B点的动能为
![]()
解得![]()
物块经过BC次数
![]()
设物块最终停在距离C点x处,可得
![]()
代入数据可得
![]()

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案【题目】某实验小组利用拉力传感器和速度传感器探究“动能定理”,如图所示,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小。在水平桌面上相距50.0cm的A、B两点各安装一个速度传感器记录小车通过A、B时的速度大小。小车中可以放置砝码。

(1)本实验是否需要平衡摩擦力____________。
实验主要步骤如下:
①测量________和拉力传感器的总质量M1;把细线的一端固定在拉力传感器上,另一端通过定滑轮与钩码相连;正确连接所需电路;
②将小车停在C点,释放小车,小车在细线拉动下运动,记录细线拉力及小车通过A、B时的速度;
③在小车中增加砝码,或__________,重复②的操作。
次数 | M/kg |
|
| F/N | W/J |
1 | 0.500 | 0.760 | 0.190 | 0.400 | 0.20 |
2 | 0.500 | 1.65 | 0.413 | 0.840 | 0.420 |
3 | 0.500 | 2.40 |
| 1.220 | W3 |
4 | 1.000 | 2.40 | 1.20 | 2.420 | 1.21 |
5 | 1.000 | 2.84 | 1.42 | 2.860 | 1.43 |
(2)表格是他们测得的一些数据,其中M是M1与小车中砝码质量之和,![]() 是两个速度传感器记录速度的平方差,可以据此计算出动能变化量ΔE,F是拉力传感器受到的拉力,W是F在A、B间所做的功。表格中ΔE3=__________J,W3=__________J(结果保留三位有效数字)。
是两个速度传感器记录速度的平方差,可以据此计算出动能变化量ΔE,F是拉力传感器受到的拉力,W是F在A、B间所做的功。表格中ΔE3=__________J,W3=__________J(结果保留三位有效数字)。